TTM4110: Dependability and Performance with Discrete Event Simulation
# Preface
This compendium attempts to provide a sufficent summary of the most important concepts of the course. This compendium is written by students for educational purposes and is largely based on the course book and the lecture slides of 2018.
The compendium is not written by professionals, so there are bound to be errors. If you spot any such errors, feel free to correct it. If you feel like something important is missing from the compendium, feel free to add it yourself.
# Chapter 1 Introduction
This chapter attempts to expalin what the course is all about and throws a bunch of new terms and concepts that will be further explored in the following chapters. In this chapter we will give you the most central concepts (the ones that has been asked about in previous exams) and provide an explaination of some of them.
## Systems, models and properties
This course is all about evaluating the dependability and/or performance of systems so it makes sense to start out with clarifying what that entails.
System
: A system can be defined as a regularly interacting or interdependent group of items forming a unified whole.
Basically a system can be anything that does anything, as long as there are several components working together to peform some sort of funciton.
A system can be described by two types of characteristics: functional and non-functional properties.
Functional properties
: Which functions are performed.
Non-functional properties
: How well these functions are performed.
Non-functional properties are the most important concepts in this course. Non-functional properties can be either performance (e.g carrying capacity, speed, blocking probability, delay) or dependability (the system works and fullfills its function, safety).
When evaluating the dependability and performance of a system, we often don't want to use the actual system for the evalutation. Instead we use a model of the system.
Model
: A model is an abstraction of the real or projected system.
A model is in simpler words: A simplifcation of the real system. There can be several reasons for using a model. Developing a model is most likely a lot less constly than building the actual system, and by analysing the model is is possible to discover problems, that could have been costly to fix if the system was already built. Another reason can be simplicity. Properties of a system can sometimes be difficult to handle or measure. By building a simpler model, these properties can be studied in a controlled manner. When using a model it is important to know that the results derived from the model should be valid for the real system, not just for the model.
A system has three basic properties:
System components
: System components are items that limit the dependability and/or performance of the system (e.g processors, hard disks, transmission channels).
Structure
: A reflection of how the system components interact. The structure of a system can be physical, logical, or derived from the physical and/or logical sturctures.
Behaviour
: The interactions (themselves) between the system components (e.g Queueing disciplines, protocols, other traffic mechanisms apart form protocols, fault handling).
## QoS
The book continues to introduce concepts that are required for understanding the concepts later on in the coruse, so here it goes:
Quality of Service (QoS)
: Degree of compliance of a service to the areement that exists between the user and the provider of the service.
Basically: Does the system live up to my expecations? How well does it do that?
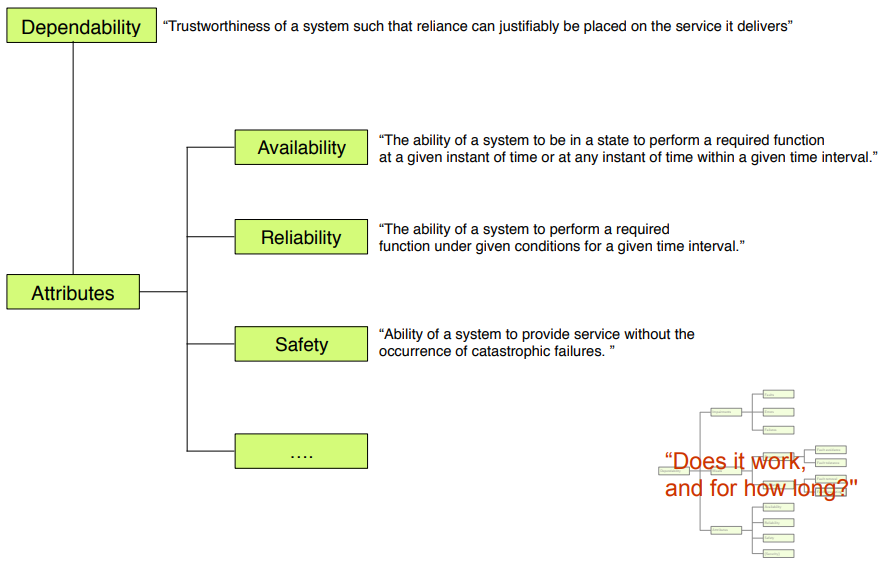
## Dependability
Dependability
: Trustworthiness of a system such that reliance can justifiably be placed on the service it delivers.
Basically: Can I trust that system works correctly when using it?
Failure
: Deviation of the delivered service from the compliance with the specification. Transition from correct service to incorrect service (e.g the service beomes unavailable).
Error
: Part of the system state which is liable to lead to a failure.
Fault
: Adjudged or hypothesized cause of an error.
These three concepts together are the threats to dependability. They are connected like this: A fault causes an error and an error may lead to system failure. There two basic appoaches to achieve a dependable system:
Fault prevention
: To prevent the occurence or introduction of faults.
Fault tolerance
: To prevent that errors cause fialures or, in other words deliver a correct service despite the presence of faults.
There are several types of faults, these are the most important to know:
Physical faults
: These are the "classical" faults, e.g physcial wear out of components.
Transient faults
: These faults are present only for a short period of time and physical change occurs in the system, e.g. external disturbances like electromagnetic interference and radiation.
Intermittent faults
: These faults come and go, for instance due to hardware components operating close to its tolerance limit, e.g. a gate that receive only sometimes (and not always) a satisfactory signal level.
MTFF
: Mean Time to First Failure
MTCF
: Mean Time to Catastrophic Failure
MTBF
: Mean Time Between Failures
MUT
: Mean Up Time
MDT
: Mean Down Time
MTTF
: Mean Time To Failure
The last major definitions related to dependability are:
Availability
: Ability of a system to provide a set of services at a given time or at any instant of time or at any instant within a given time interval.
Reliability
: Ability of a system to provide uninterrupted service.
Safety
: Ability of a system to provide service without the occurence of catastrophic
## Performance
Performance also has several definitions and concepts we must understand so bear with me:
Performance
: Abiliy of a system to provide the resources needed to deliver its services.
Capacity
: Maximum load a syste mcan handle per time unit.
Carried traffic
: Average number of resources in a time interval. Measured in Erlang.
Primary traffic
: Traffic generated by the users.
Secondary traffic
: Traffic used for signalling between network nodes.
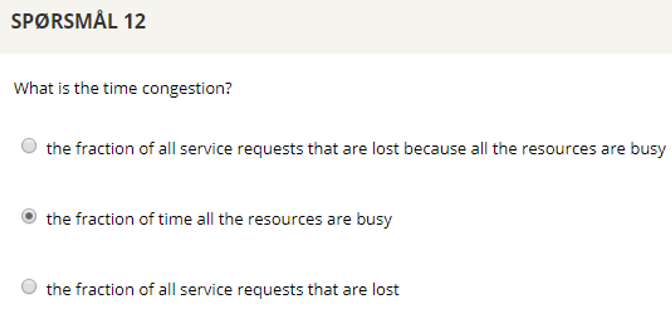
Time Congestion
: The Fraction of tiem all resources are busy.
Throughput
: Portion of the system capaciy that is utilised be the users.
Delay
: Time it takes to complete a service.
Waiting time
: Accumulated time a service request is pending for service in a system.
Service time
: Accumulated time a servide request is served by a system.
Sojourn time
: Total time a service request is in a system.
## Methods:
There are three primary ways of analysing a system: Mathematical analysis, simulation and measurement on a prototype of a system. Here are the main benefits of each of them:
Mathematical analysis
: In the case of well-known problems, results can easily be obtained using formulas or algorithms.
Simulation
: Relatively detailed models can be used.
Measurements on (a prototype of) a system
# Chapter 2: Fundamentals of probability
Not completed yet, feel free to contribute here.
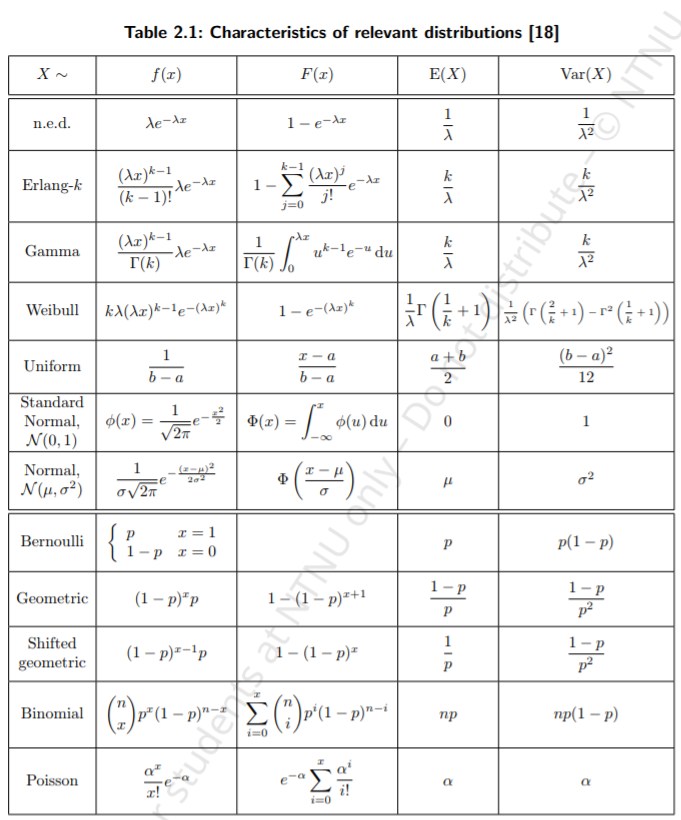
__Expected value__: $ µ = E(X) $
__Sample mean (avarage)__: $ µ \approx \overline{X} = \frac{1}{n} \sum_{i=1}^n X_i $
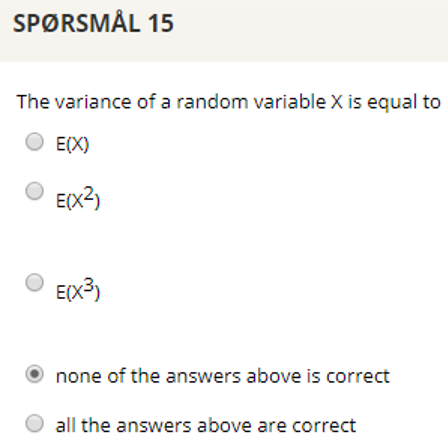
__Variance__: $ σ^2 = Var(X) = E[(X-µ)^2] = E(X^2) - µ^2 $
__Sample variance__: $ S^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i-\overline{x})^2 $
$ S^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i^2 - 2\overline{x}x_i + \overline{x}^2)^2 $
$ S^2 = \frac{1}{n-1} \sum_{i=1}^n x_i^2 - 2\overline{x}\sum_{i=1}^nx_i + n\overline{x}^2 $
$ S^2 = \frac{1}{n-1} \sum_{i=1}^n x_i^2 - n\overline{x}^2 $
__Standard deviation__: $ σ = \sqrt{Var(X)} $
__Standard error__: $ SE = \sqrt\frac{σ^2}{n} = \frac{σ}{\sqrt n} ≈ \frac{S}{\sqrt n} $
__Intensity__: $ E(X) = \frac{1}{γ} \rightarrow E(\hat{X}) = \hat{γ} $
__Conditional probability__: $ P(A | B) = \frac{P(A ∩ B)}{P(B)} $
__Baye's formula__: $ P(A | B) = \frac{P(B | A) · P(A)}{P(B)} $
__Negative exponential distribution (n.e.d) (probability density function)__:
$ f(x) = λe^{−λx} $
or cumulative: $ F(x) = 1 − e^{−λx} $
__Erlang -k distribution probability density function
(k is shape and λ is rate of each phase)__:
$ f(x) = \frac{(λx)^{k−1}}{(k − 1)!} λe^{−λx} $
and cumulative:
$ F(x) = 1 − e^{−λx} \sum_ {j=0}^{k-i} \frac{(λx)^j}{j!} $
__Death rate (failure rate)__:
$ φ(t) = \frac{f(t)}{1 − F(t)} $
# Chapter 4: Simulation
## Simulation
Imitative representaion of the functioning of one system or process by means of the functioning of another.
In the context of this course: A simulation is performed by means of a software program, called a simulator, running on a computer. By simulation, we really mean stochastic simulation where the behaviour of the system components is, fully or partly, governed by stochastic processes. To imitate a stochastic behavior, the simulator, and therefore the computer, has to be able to generate random variables according to a given probability distribution.
### Random variable generation:
Simulation reilies on the generation of random variables, and therefore on the generation of random numbers. Generated random variables are called _random variates_. Random numbers may be generated either from a physical process or from an algorithm. The main drawback of generating random numbers from a physical process is that the sequence is not reproducible. Generating random numbers from an algorithm using a computer allows to generate a large amount of numbers and to reproduce the same sequence several times which enables to reproduce the same experiments. Random numbers generated by an algorithm are not truly random since the algorithm itself is deterministic and are therefore called _pseudo-random numbers_. However, the sequence of numbers generated should appear to be _statisically random_ (independent and uniformly distributed random numbers).
Requirements: Fast (many samples), portable, long cycle period, reproducible sequences, good statistical properties.
#### Direct method:
__Pro__: Fast, empirical distribution
__Con__: Only applicable to discrete distributions.
#### Inverse Transform:
__Pro__: Fast
__Con__: Distributions require a closed form inverse transform.
#### Acceptance-Rejection:
__Pro__: Many distributions.
__Con__: Many samples per random variate generated.
#### Convolution:
__Pro__: Simple implementation of complicated distributions.
__Con__: Only applicable to sum of variates.
## Advantages and disadvantages of simulation
Simulation is a flexible and practical way of analyzing systems. Simulation allows to make models that include exactly the necessary level of granularity, not more not less. A simulation model is better tailored for a given study than a mathematical model or a real system. A mathematical model often needs to be prohibitevely simplified to be solved analytically. A real system used for a measurement study can obviously not be simplified at all.
A simulation model is often more challenging and more demanding with respect to the insight into the system and the understanding of its operation. One must be able to remove unnecessary details and at the same time understand and describe the details of importance for a given study. Hence, a common and important by-product of a simulation study is an improved insight into the system and the identification of possible weaknesses in the design.
## Types of simulation models
Simulation can be classified as static or dynamic, discrete or continuous, and deterministic or stochastic.
In this course we use dynamic, discrete, and stochastic simulation models.
### Static simulation model
Also called Monte-Carlo simulation models a particular point in time (time not part of model) E.g throwing a dice.
### Dynamic simulation model
Model represents a system as it changes over time. E.g. simulate a bank from 08:00-16:00.
### Discrete simulation model
State variables change only at discrete set of points in time.
### Continuous simulation model
State variable changes continuously over time.
### Deterministic simulation model
Contains no random variables.
### Stochastic simulation model
Contains at least one random input variable
## Discrete event simulation (DES):
The system dynamics is given by discrete events. The system state is distinct and will only change at a specific time instance. Simulations of discrete events need only to simulate the events that change the system state, and a finite number of events will take place in a finite interval of time.
## Time driven vs. event-driven simulation:
Time driven: Fixed time stamp. For example: Move the clock 1 second forward and determine the system state.
Event driven: Variable time-stamp. For example: Move the clock to the time of next event.
## Concepts in Discrete event simulation:
__Model__: Abstract representation of system.
__Entity__: Object with explicit model description.
__Attributes__: Properties of an entity.
__System__: Collection of entities.
__System state__: Set of variables containing sufficient information.
__List__: Collection of associated entities.
__Event__: Change of system state.
__Event notice__: A record of an event to occur.
__Event list__: List of event notices (ordered by time)
__Activity__: Specified duration.
__Delay__: Unspecified duration.
__Resource__: Passive object used to perform an activity.
## Process oriented simulation:
A Process describes the behaviour of an entity (sequence of activities, life cycle). Focus on the entities and their dependencies and interactions (object-oriented approach). Event-driven approach. Requires a list of events and synchronization mechanisms.
## Activity diagram:
A graphical representation of a model. Activites/life-cycles of entities. Interactions between entities (cooperation, interrupt, generation, priorities). Entities and resources (comptetition, synchronization).
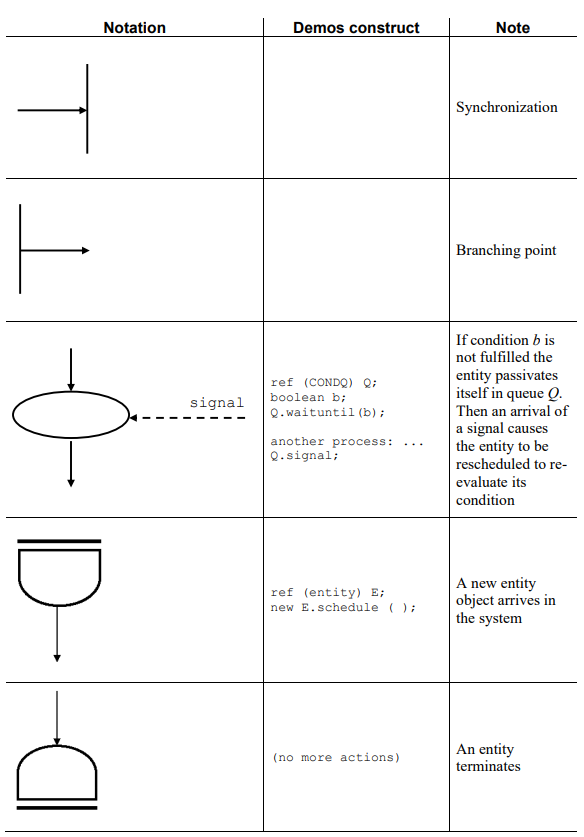
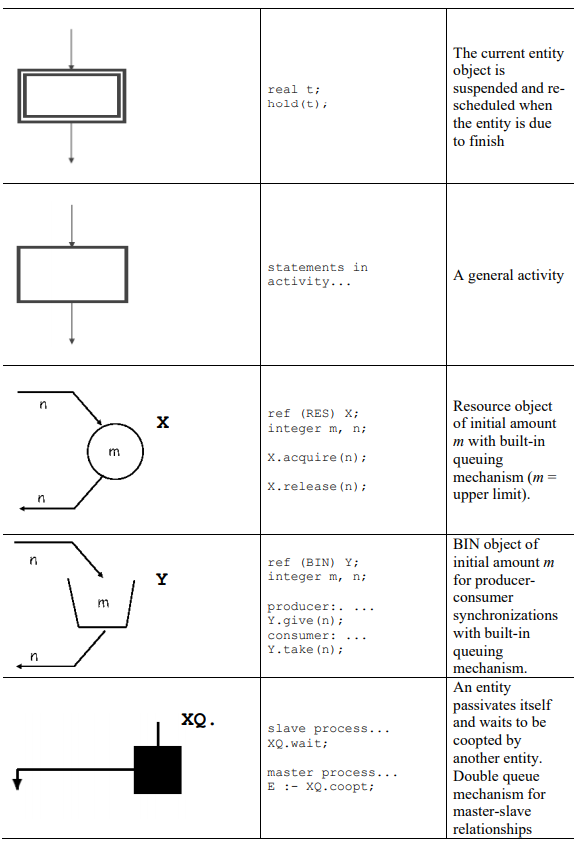
# Chapter 5: Traffic Models
This chapter presents the Poisson process and its properties. In particular, it describes how Poisson processes can be aggregated to form Markov processes that are an important part of Markov models.
## Poisson and Markov Process
__Poisson process__: Regular point process (only one event at the time). Intensity is constant (homogenous PP). Intensity is independent of previous events.
__Markov process__: Events from many Poisson Processes.
__Poisson distribution__: Number of events until and including time t.
__Exponential distribution__: Time between two consecutive events.
### Poisson process -merging
The merging (superposition, multiplexing) of two Poisson processes is a Poisson process.
Splitting of a Posson process in n processes forms n Poisson processes if the splitting is probabilitstic (with constant probability).
## Stationary traffic models
### Examples of queuing systems
Phone subscirbers share a limited number of telephone lines in a telephone exchange
Mobile phone subscribers share a limited number of radio transmitters/receivers in a mobile base station.
Taxi call centers have delay queues.
IP routers have input and output buffers.
Maintenance centers have order lists and repairmen.
__Performance__: Delay, blocking, utilization, waiting time...
### Queuing model
A system does not need to have any queuing positions to be classified as a __queuing system__.
A queueing system is characterized by the arrival process, service time distribution, number of servers, maimum number of customers in the system, number of sources, and queuing dicipline (service order).
# Random extensions
## Use of modeling in development and dimensioning.
TODO
__Point process__
- Point process describes occurrence of an event
- No gradation of type of event
- The state, X(t), of a process is the number of events, N(t)
_Regular point process_ only one event at a time.
> Time to k'th event:
$$ S_k = \sum_{i=1}^k Y_i $$
har også at
$$ P(N(t)<k) = P(S_k>t) $$
sd
__Renewal process__
Regular point processes
Time to next event is independent of what happened in the past
The superposition of merging two renewal processes is generally __not__ a renewal process.
However, the superposition of a large number of renewal processes tends to a Poisson process.
__Little's formula__:
$$ \overline{N} = λ\hat{W} $$
N is avarage for N(t).
W is avarage for all
__Erlang__: Erlang is a dimensionless unit that is used as a measure for offered load or carried load from service-providing elements.
Often expressed as call arrival rate times average call length.
Given a scenario with a single cord in telephone system. The cord can provide phone calls for 60 minutes per hour. A full utilization of the cord results in 1 erlang.
If users now attempts to make calls in this system (measured in eg. per hour):
* Carried load is the traffic that was carried for the successful call-attempts.
* Offered load is the traffic that would have been carried if all the call-attempts succeeded.
Offered traffic (in erlangs) is related to the call arrival rate, λ, and the average call-holding time (the average time of a phone call), h, by:
$$ E = λh $$
provided that h and λ are expressed using the same units of time (seconds and calls per second, or minutes and calls per minute).
__Relative frequency__:
Number of times the event occurs divided by the number of
times an experiment is carried out
__Probability__:
Asymptotic relative frequency of the event investigated
__Joint probability__:
The probability that both events occurs in conjunction
(Intersection) $ P(A ∩ B) $
__Conditional probability__:
If A and B are two events, and P(B) > 0
P(A|B) = P(A ∩ B)
P(B)
Multiplicative rule
P(A ∩ B) = P(A|B)P(B)
Law of total probability:
P(B) = P
j P(B ∩ Aj) = P
j P(B|Aj) · P(Aj)
__Negative exponential distribution__:
X ∼ Exp(λ)
$$ f(x) = λe^{−λx}, x ∈ R^+ $$
$$ F(x) = 1 − e^{−λx} $$
where $λ ∈ R^+$ is the rate parameter
__Erlang-k distribution__: It is the distribution of the sum of k random variables identically distributed.
X ~ Erlang-k(λ)
$$ f(x) = \frac{(λx)^{k−1}}{(k − 1)!} λe^{−λx}$$
Der $x ∈ R^+$
__Binomial distribution__:
Probability distribution of the number X of events 1 in a
sequence of n independent Bernoulli trials.
X ∼ Bin(n, p)
$$f(x) = \binom{n}{x} p^x (1-p)^{n-x} $$
Der $x ∈ $ {0, 1, ...}
__Poisson distribution__:
Corresponds to the binomial distribution with an infinite number
of Bernoulli trials.
Probability of the number of occurrences of an event, given
that it occurs on average at the intensity $α ∈ R^+$
X ∼ P(α)
$$ f(x) = \frac{α^x}{x!} e^{-α} $$
$x ∈ N$
__Poissoon process__:
> TODO: format
• Regular point process (only one event at the time)
• Intensity is constant (homogeneous PP)
• Intensity is independent of previous events
The merging (superposition, multiplexing) of two Poisson
processes is a Poisson process
Splitting of a Poisson process in n processes forms n
Poisson processes if the splitting is probabilistic (with
constant probability)
## Queueing model
### Kendall's notations:
> TODO: format
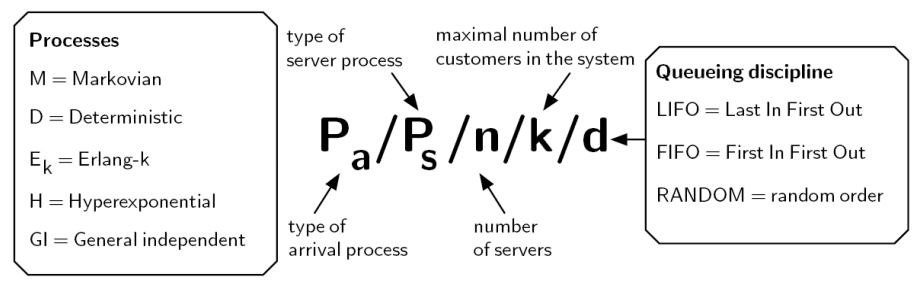
__Examples__
Kendall’s notation, example: M/M/1
– M = Poisson arrival process
– M = service time distribution is n.e.d.
– 1 server
– No system capacity given, i.e. infinite
– No queuing discipline, i.e. arbitrary discipline can be
used
• Infinite server systems: M/M/∞
• Loss systems: M/M/n/n
• Delay systems with infinite queue: M/M/n
• Jackson’s queueing network: network of M/M/nj -system
## Dependability
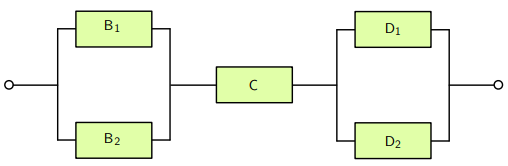
### Series system:

__Availability__: $$ A_{series} = \prod_{i=1}^n X_i $$
__Reliability function__: $$ R_{series}(t) = \prod_{i=1}^n R_i(t) $$
der $ R_i(t) = e^{-λ_it} $
### Parallel system:
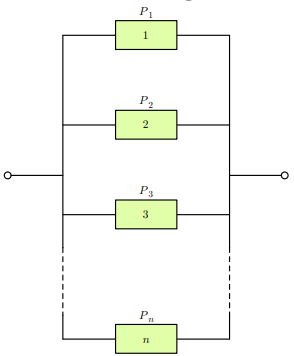
__Availability__: $$ A_{parallel} = 1 - \prod_{i=1}^n (1-X_i) $$
__Reliability function__: $$ R_{parallel}(t) =1 - \prod_{i=1}^n (1-R_i(t)) $$
### K-of-n system:
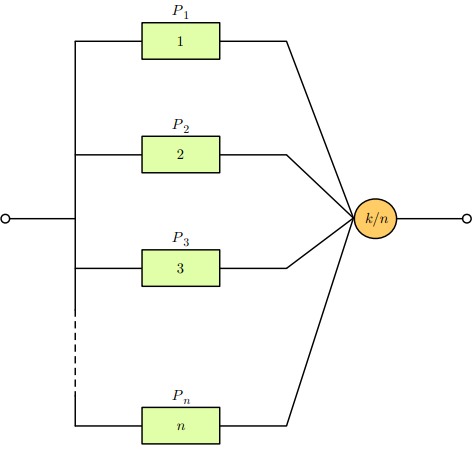
__Availability__:
$$ A_{k-of-n} = \sum_{i=k}^n \binom{n}{i} A^i (1-A)^{n-i} $$
__Reliability function__:
$$ R_{k-of-n}(t) = \sum_{i=k}^n \binom{n}{i} R(t)^i (1-R(t))^{n-i} $$
### Mean Time to First Failure:
$$ MTFF = E(T_{FF}) = \int_0^∞ R(t)dt $$
### Mean Time to Catastrophic Failure:
$$ MTCF = E(T_{CF}) $$
### Mean Time Between Failures:
$$ MTBF = E(T_{BF}) $$
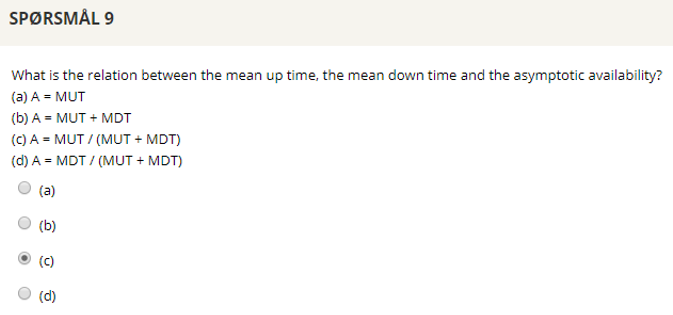
### Mean Up Time:
$$ MUT = E(T_U) $$
### Mean Down Time:
$$ MDT = E(T_D) $$
### Mean Time To Failure:
$$ MTTF = E(T_F) = \int_0^∞ R(t) dt $$
### Mean Time to First Failure:
For a system that cannot be repaired and a structure of
independent elements with constant failure rate $λ_i$ $(λ = λ_i, ∀i)$.
$$ MTFF_{series} = (\sum_{i=1}^n λ_i)^{-1} $$
$$ MTFF_{parallel} = \frac{1}{λ} \sum_{i=1}^n \frac{1}{i} $$
$$ MTFF_{k-of-n} = \frac{1}{λ} \sum_{j=k}^n \frac{1}{j} $$
### How to improve system availability:
- Identify the most critical factor (element) in the system model
- Set element availability to 1
- Calculate the net change in system availability
- Repeat for all elements
- Which element has the larges impact on the system availability?
- What does it take to improve that element?
- Alternatives:
- Replacement of a component with lower failure rate
- Improve recovery time
- Change the structure by adding more
## Cut set
__Cut set__
> The system fails if all elements in the set fails
__Minimum cut set__
> The system fails if and only if (iff) when all elements in the set fail,
given that the system elements not in the set are working
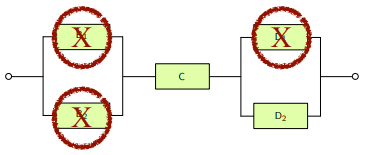
## Path set
__Path set__
> The system is working if all elements in the set are working
__Minimum path set__
> The system is working iff all elements in the set are working,
given that all system elements not in the set are failed.
### Example:
# Selftest 1:
## Question 1

## Question 2
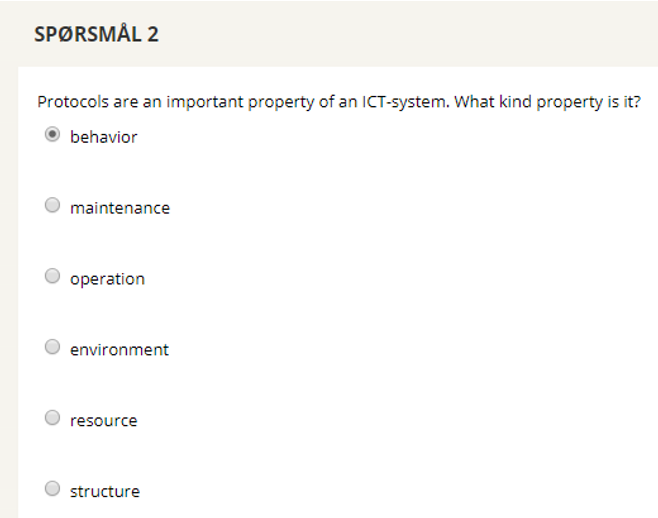
The main purpose of a protocol is to provide rules for the different entities in a system/network to cooperate. In other words a protocol dictates how various system parts interact with eachother, and is thus part of the __behaviour__ property of the system.
## Question 3

Definition from the book: Quality of Service (QoS) is the degree of compliance of a service to the agreement that exists between teh user and the provider of this service.
## Question 4
## Question 5

## Question 6

## Question 7

## Question 8

## Question 9
## Question 10

## Question 11

## Question 12
## Question 13

## Question 14

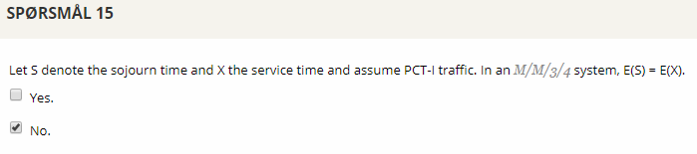
## Question 15
## Question 16

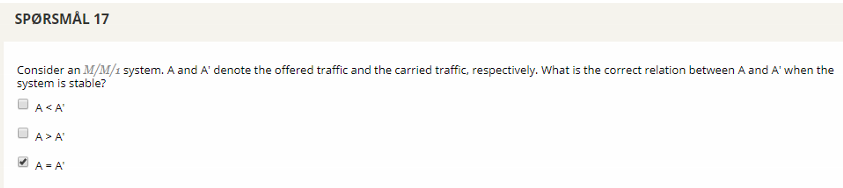
## Question 17

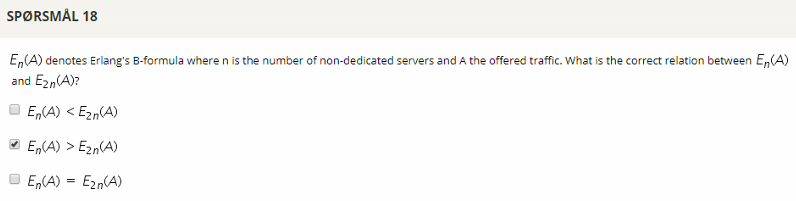
## Question 18
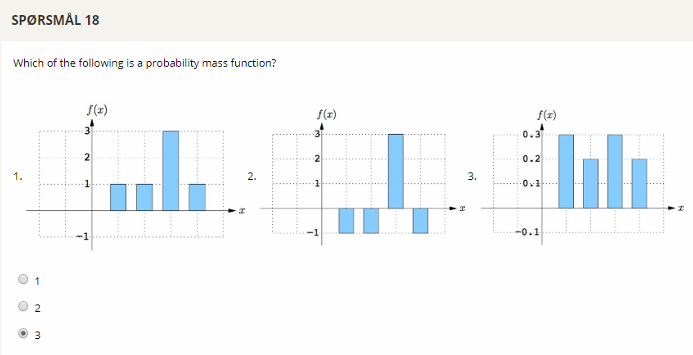
Individual probabilities must be between 0 and 1. The sum of all probabilities must equal 1.
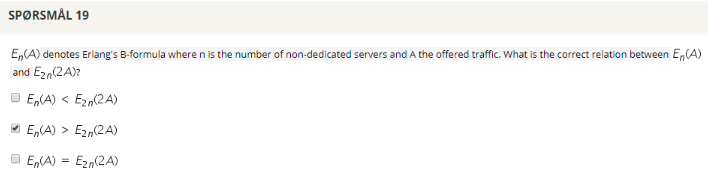
## Question 19

## Question 20

## Question 21
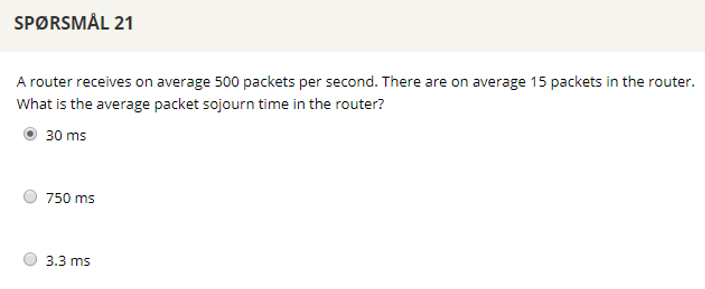
15/500 = 0.03
# Selftest 2
## Question 1

## Question 2

## Question 3

## Question 4
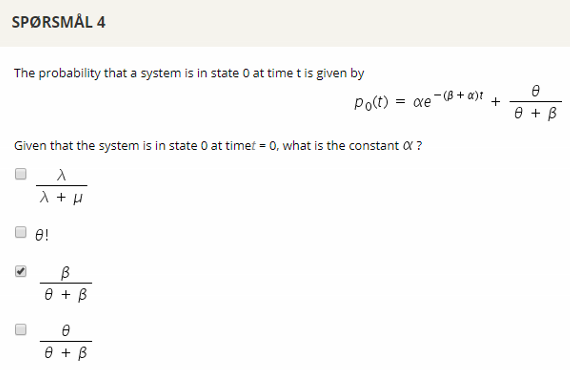
## Question 5

## Question 6

## Question 7

## Question 8

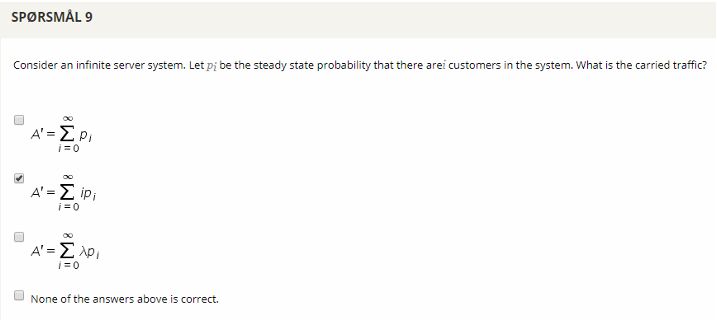
## Question 9
## Question 10

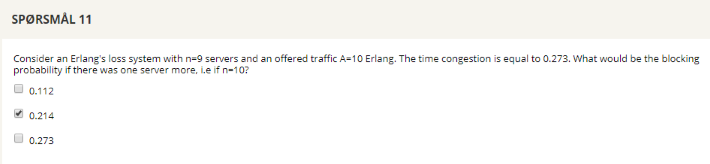
## Question 11
## Question 12

## Question 13

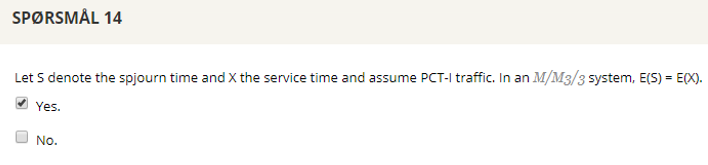
## Question 14
## Question 15
## Question 16

## Question 17
## Question 18
## Question 19
## Question 20
