TDT4300: Datavarehus og datagruvedrift
Datavarehus vs Datagruvedrift
Vi bruker datavarehus til å oppbevare og bearbeide kjente data. Dette betyr ikke nødvendigvis at vi vet alt om dataene, og ved å bruke datavarehus kan vi hente ut resultater vi ikke hadde fra før.
I datagruvedrift er målet å oppdage ny informasjon. Vi benytter oss av de dataene vi har til å trekke slutninger som vi ikke kunne trekke tidligere. Et eksempel på dette er at vi kan lære at hvis en kunde kjøper både aviser og bleier vil kunden også komme til å kjøpe øl.
Datavarehus
- Data warehouse
- A data warehouse is subject-oriented, integrated, non-volatile, time-variant data collection organized in support of management decision making
"Subject-oritented" vil si at data samlingen er organisert rundt vitkige emner/tema som kunder, produkter, salg. Det er fokus på modellering og analyse av data for beslutningstagere, IKKE daglige operasjoner eller transaksjoner. Gir en enkel og konsistent oversikt over aspekter ved emnene, ved at data som er uvesentlgie for beslutningene utelates.
"integrated" vil si at data samlingen konstrueres ved å integrere data fra mange forskjellige kilder (relasjonsdatabaser, dokumenter, eksterne kilder, etc.). Data vaskes og det brukes teknikker/metoder for å integrere dataene.
"non-volatile" vil si at data samlingen er et fysisk separat lager av data som er transformert fra operasjonelle data. Ingen operasjonelle oppdateringer (f.eks. ingen endringer ved de daglige transaksjonene). Ingen transaksjonshåndtering, recovery eller concurrency control. Valigvis kun behov for to data-aksess-operasjoner: Lasting av data og tilgang til data.
"time variant" vil si at tidshorisonten for datavarehus er vesentlig legnre enn for et operasjonelt system. En operasjonell database gir kun nåværende dataverdier. Data i dataverhus gir informasjon i et historisk perspektiv (type 5-10 år). Alle data i et datavarehus har elementer av tid, eksplisitt eller implisitt. Selv om nøkkelattributtene ikke bestanding inneholder tidsattributt.
Bruk av datavarehus har som mål å hjelpe oss til å samle inn data, modellere, lagre og gjøre disse dataene tilgjengelig for analyse. Datavarehus brukes til modellering av data for besluttningstakere, og ikke til de daglige operasjonene i en bedrift. Dataene er dermed ikke nødvendigvis helt oppdaterte. I stedet oppdateres de med jevne mellomrom, eller on-demand. Dataene i et datavarehus er organisert rundt temaer eller emner, som kunder, produkter, eller salg.
Et datavarehus integrerer data fra en rekke kilder. Det kan være tradisjonelle relasjonsdatabaser, diverse dokumenter eller annet. Før de settes inn i datavarehuset må dataene vaskes slik at de er kompatible og konsistente.
Tidshorisonten i datavarehus er svært lang, og kan inneholde historiske data for de siste 5-10 år.
Fordelen med at dataene ikke er operasjonelle (altså de helt oppdaterte dataene) er at vi ikke trenger å ta hensyn til transaksjonskontroll og gjennoppretting. Vi trenger kun å kunne laste inn data, og prosessere dem. Dette gjør det mye enklere å drifte datavarehuset.
Datavarehus er en type teknologi som kalles Online analytical processing ( OLAP ). Dette står i motsetning til Online transaction processing ( OLTP ), som operasjonelle databaser normalt sett er. Fordelen med OLAP-systemer er at de kan svare på komplekse spørringer, og at man kan jobbe med multidimensjonale data langt mer effektivt. Det utvikles systemer som gjør det mulig å gjøre OLAP mot operasjonelle databaser.
OLAP vs OLTP
| OLTP | OLAP | |
| Brukere | Kontorfolk, IT | Kunnskapsarbeider (analytiker etc.) |
| Funksjon | Dag-til-dag operasjoner | Beslutningshjelp |
| DB-design | Applikasjonsorientert | Subjektorientert |
| Data | Nåværende, detaljert, flat | Historisk, summert, multidimensjonell |
| Bruk | Repetitiv | Ad-hoc |
| Tilgang | Read/write, indeksering/hashing på primærnøkkel | Mye søking |
| Arbeidsenhet | Korte, enkle transaksjoner | Komplekse spørringer |
| # aksesserte poster | Titalls | Millioner |
| # brukere | Tusener | Hundretalls |
| DB-størrelse | 100MB-GB | 100GB-TB |
| Målt ved | Gjennomstrømning av transaksjoner | Gjennomstrømning av spørringer, respons |
Datavarehusmodeller
Det er i hovedsak 3 typer datavarehusmodeller:
- Enterprise varehus
- Inneholder data om alle emner for hele virksomheten.
- Gjerne den overordnede samlingen av alle data firmaet er i besittelse av.
- Datamart
- Et datamart er et subsett av datavarehuset som inneholder data som tematisk eller analytisk passer sammen. Typisk vil en avdeling som arbeider med f.eks. salg være lite interessert i statistikken over ansattes fravær. Derfor vil vi skape et datamart som inneholder kun den informasjonen som er relevant.
- Virtuelle varehus
- Dette er et datavarehus som er skapt virtuelt på toppen av operasjonelle data.
- Vi kan her oppleve begrensninger i hva vi kan få til, da det er begrensninger i den operasjonelle databasen.
Datavarehusprosesser
Omtales ofte som ETL (Extract-Transform-Load)
- Dataekstrahering
- Henting av data fra ulike kilder
- Datavasking
- Tilpasse data til det systemet de skal inn i
- Oppdage feil i data, rette dem hvis det er mulig
- Datatransformering
- Konverter til datavarehusets formater
- Innlasting
- Sorter, summer, konsolider, sjekk integritet, indekser, partisjoner
- Oppdater
- Oppdater datavarehuset med nye data fra det operasjonelle systemet
- Gjøres periodisk, ikke kontinuerlig
Datakube
En datakube er en flerdimensjonal modell av dataene våre. I en vanlig relasjonell database representeres data i en todimensjonal tabell. Fordi vi i datavarehus ofte trenger å se sammenheng mellom mer enn to dimensjoner av dataene våre velger vi å representere dem som en n-dimensjonale kube. Denne kaller vi for en datakube eller hyperkube.
I en datakube representerer hver dimensjon ett av datasettets attributter. I kontekst av en salgsdatabase vil typiske attributter være salgstid, kjøpesum, selgerID, produktkategori etc.
Gitt en datakube med n dimensjoner kan man generere rektangulære bokser basert på subsett av dimensjoner i datakuben. Slike bokser kalles kuboider. Eksempel: i en datakube med dimensjoner tid, produkt og kunde kan følgende kuboider genereres: {{alle}, {tid}, {produkt}, {kunde}, {tid,produkt}, {tid,kunde}, {produkt,kunde}, {tid,produkt,kunde}}. Antall kuboider i en datakube med n dimensjoner er gitt ved 2^n.
Modellering av datavarehus
Når vi skal modellere et datavarehus må vi ofte ty til andre teknikker enn ved modellering av typiske OLTP-systemer. Vi benytter oss fortsatt av konseptene tabeller og nøkler fra tradisjonell databasemodellering, men bruker andre oppsett av data.
Stjerneskjema
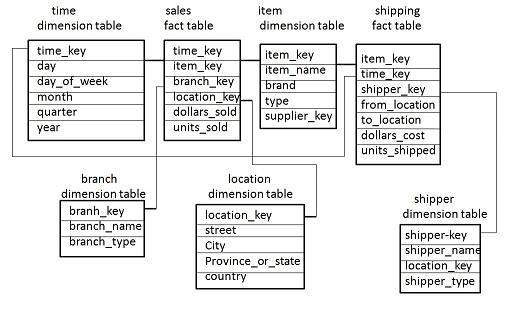
Et stjerneskjema benytter seg av en sentral faktatabell med alle verdiene vi er interessert i. Vi har en tabell for hver dimensjon, som er knyttet til faktatabellen med nøkler. Det finnes kun ett nivå, alle tabeller er altså direkte knyttet til faktatabellen. En følge av dette er at vi ikke vil kunne normalisere alle data. Dette kan i teorien skape stor redundans, men er ofte ikke et stort problem. En stor fordel er at dataene ikke må joines for hver spørring, noe som sparer mye tid.
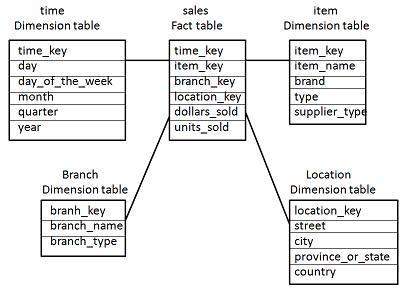
Snøflakskjema
En utvidelse av stjerneskjemaet som tillater at noen dimensjoner normaliseres, dvs. at vi kan ha dimensjonstabeller som ikke er direkte knyttet til faktatabellen vår. Vi får en mer eksplisitt hierarkisk organisering av dimensjonene.
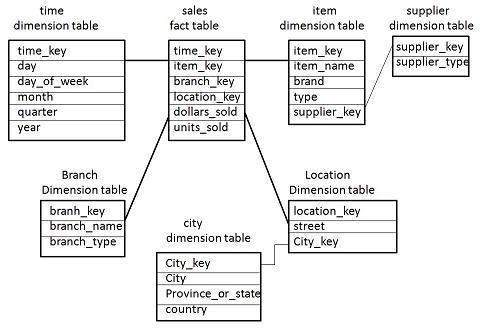
Faktasammenstilling
Hvis vi setter sammen flere snøflakskjema og/eller stjerneskjema vil vi få en faktasammenstilling. Her er det typisk flere faktatabeller, og disse kan dele på dimensjonstabeller. Vi kan også kalle dette for et galakseskjema eller galaxy schema.
Konsepthierarkier
Når vi utfører analyse på data i et datavarehus er vi ofte interessert i ulik granularitet på dataene. En måte å realisere dette på er å bruke konsepthierariker. Et eksempel på et konspethierarki vil være måten vi strukturerer tid på. Et år er bygd opp av 12 måneder, som igjen er bygd opp av 28-31 dager, som igjen er bygd opp av 24 timer osv. Når dette er definert i datavarehussystemet vårt kan vi lett bevege oss mellom ulike nivåer i hierarkiet, og på den måten aggregere data til det ønskede nivået.
Konsepthierarkier kan både være strikte hierarkier (se på det som et tre) eller i form av et gitter. Det viktigste er at hierarkiet er ordnet i en rekkefølge.
Beregninger i datavarehus
Vi kan i et datavarehus gjøre forskjellige beregninger. Ofte må vi gjøre disse når vi skal aggregere data til nye nivåer i konsepthierarkier. Det er i hovedsak tre typer beregninger, og det som skiller dem er hvor lett de er å distribuere mellom flere prosesser.
- Distribuert aggregering
- Her kan hele beregningen gjøres distribuert. Vi kan dele opp settet i delsett, og la ulike prosesser beregne hver sin del.
- Når hver prosess kommer tilbake med svaret sitt kan vi gjøre samme operasjon på delsettene.
- Algebraisk aggregering
- Her har vi funksjoner som har M argumenter, og hvor hvert argument er mulig å beregne med distribuert aggregering.
- Gjennomsnitt = Sum / Antall
- Sum og antall er i seg selv algebraisk distribuerbart
- Holistisk
- Disse funksjonene må gjøres på hele settet hvis beregningen skal være korrekt
- Median, rank, modi.
OLAP-operasjoner
Når vi skal aggregere data i en datakube har vi et sett av operasjoner tilgjengelig.
- Roll-up
- Vi beveger oss oppover i konsepthierarkiet
- Dette blir i praksis en reduksjon i dimensjoner
- Data må aggregeres for å stemme med det nye nivået i hierarkiet
- Drill-down
- Motsatte av roll-up
- Krever at vi har tilgang på data fra en lavere grad i konsepthierarkiet
- Slice
- Velg ut en dimensjon, og skap en subkube.
- Normalt sett en todimensjonal kube (derav slice)
- Dice
- Velg ut en subkube med to eller flere dimensjoner
- Pivot
- Roter dataene slik at aksene omorganiseres
Spørringer
OLAP-spørringer kan foregå gjennom enten en utvidelse til SQL, eller gjennom et eget spørrespråk, f.eks. MDX (MultiDimensional eXpressions).
OLAP-implementasjoner
ROLAP
Relational OLAP-servere bruker relasjonsdatabaser som backend og implementerer aggregering på toppen av dette. Lagrer data svært effektivt, men er krevende å optimalisere.
MOLAP
Multidimensional OLAP-servere bruker arraybaserte filsystemer, og opererer internt med en datakubestruktur. Indeksering er effektiv, men lagringsutnyttelsen er dårlig hvis dataene har mange tomme felt.
Indeksering
Indeksering i OLAP-systemer er en utfordring, da faktatabellene ofte har mange indekser. Vi kan benytte oss av bitmap indeksing. Dette er lite lagringskrevende, og effektivt ved få verdier. Ved store verdier vil vi fort måtte lagre mange gigabyte med data for bitmaptabellen.
Vi kan også benytte en join-indeks. Her registrerer vi i en egen tabell hvilke attributter i databasen som det er mulig å utføre en join-operasjon på. Dette sparer oss beregningstid når den egentlige operasjonen skal utføres.
Det er mulig å kombinere disse metodene til bitmapped join indecies.
Datamining
Datamining er prosessen hvor man ved bruk av eksisterende informasjon finner ny informasjon. Dette er typisk at man utleder sammenhenger som man ikke tidligere var klar over, og som man ved en overfladisk inspeksjon av dataene ikke kan oppdage.
Datamining kan grupperes i:
- Predikering - Forutse fremtidige eller ukjente data basert på eksisterende data
- Klassifisering
- Avviksdeteksjon
- Regresjon
- Beskriving (deskriptiv) - Finne mønster som kan skildre data
- Klyngeanalyse
- Assosiasjonsanalyse
- Sekvensmønster
Data
Data og attributter
Data er en samling av data-objekter og deres attributter. Et attributt er en egenskap ved et objekt. En person kan f.eks. ha attributtene høyde, vekt, øyenfarge osv. Vi har flere typer attributter:
- Nominelle
- bare navn f.eks ID-nummer, farger, postkoder, stedsnavn
- Odrinale
- rangeringer f.eks Tallskalaer, bokstavskalaer, kategorier {høy, middels, kort}
- Intervall
- Datoer, temperaturer (celsius og fahrenheit)
- Forholdstall (ratio)
-
- Tid, tellinger, beløp, temperatur (kelvin)
Attributtypene kan deles i to grupper: Nominelle og ordinale er kategoriske (kvalitative), ofte diskrete verdier. Intervall og forholdstall er numeriske (kvantitative), ofte kontinuerlige verdier.
Attributtegenskaper
Vi kan utføre forskjellige operasjoner på forskjellige attributter. Dette avhenger av hvilke egenskaper attributtene har.
- Nominelle attributter: Kan utføre distinkthetsoperasjonen ("=", "!=")
- Ordinale attributter: Kan utføre distinkthets- og rekkefølgeoperasjoner ("<", ">")
- Intervallattributter: Kan utføre distinkthets-, rekkefølge- og adderingsoperasjoner ("+", "-")
- Ratioattributter: Kan utføre alle de foregående, og multiplisering og dividiering.
Attributter kan være enten symmetriske eller asymmetriske. En asymmetrisk attributt tar kun hensyn til om verdien er tilstedeværende. F.eks. er vi kun interessert i kunder som kjøper noe, så kunder med tom handlevogn oversees av systemet.
Antallet dimensjoner påvirker hvor lett det er å behandle dataene våre. Hvis vi får for mange dimensjoner kan det bli svært vanskelig å håndtere dataene. Vi får ytelses- og plassproblemer, som ofte refereres til som the curse of dimensionality.
Organisasjon av data
Dataene kan organiseres i en rekke former. De vanligste er som post, graf, eller ordnet.
Post
Vi kan organisere data som en samling av poster, hvor hver post har et fast sett attributter. Dataene kan representeres som en m*n-matrise, og kan representere et punkt i m-dimensjonalt rom.
Vi kan lage et dokument som en vektor av termer i en post. På denne måten blir verdien av hvert attributt antallet ganger det gitte ordet forekommer i teksten.
Transaksjonsdata kan også lagres som en post, da inneholder posten et sett av enheter som hører sammen.
Graf
Her organiseres data som noder med relasjoner. En lenke mellom to noder indikerer en form for forbindelse mellom dataene. Vi kan traversere grafen effektivt, og dermed finne informasjon om sammenhenger svært raskt.
Ordnede data
Her har vi data som er relatert til tid. Det er altså en rekkefølge i dataene som er relevant. Vi kan ordne en brukers transaksjoner i systemet over tid, eller logge temperaturer på forskjellige steder over tid.
Datakvalitet
I arbeidet med store mengder informasjon vil vi komme over data som ikke er av den ønskede kvaliteten. Dette kan komme av en rekke ulike årsaker. Det er utviklet ulike metoder for å forbedre dataene.
Støy
Støy er unøyaktigheter eller feil i målingene. Dette kan forekomme ved overføring av analoge signaler, eller ved målfeil og andre feilkilder.
Outlier
En outlier er et datapunkt som har en signifikant forskjell fra resten av objektene i datasettet. Dette er forskjellig fra støy ved at det ikke er noe feil i målingen, men at det reelle datapunktet befinner seg langt unna resten av målingene.
Manglende verdier
Vi kan mangle data i settet vårt. Dette kan være at en måling ikke har blitt foretatt, at noen attributter ikke gir mening for dette tilfellet (barn har neppe inntekt), eller lignende tilfeller.
Vi kan håndtere dette ved enten å fjerne objekter som ikke har alle attributter, erstatte attributter som mangler med enten et estimat eller med den mest sannsynlige verdien. Vi kan også benytte oss av dataene, men kun ignorere de manglende attributtene.
Duplikate data
Duplikate data kan forekomme hvis vi slår sammen data fra ulike kilder. Vi kan også komme til å gjøre dobbeltregistreringer. Problemene oppstår hvis man registrerer tilnærmet duplikate data, men med enkelte forskjeller. Et eksempel kan være en person som registreres to ganger med ulikt telefonnummer.
Datapreprosessering
Før vi legger data inn i datavarehuset er det behov for å tilpasse dataene til lagring og til bruk. Dette kaller vi datapreprosessering. Vi har en rekke måter å gjennomføre dette på:
Aggregering
Vi slår sammen objekter, f.eks. på samme måte som når vi beveger oss oppover i et konsepthierarki i et datavarehus. Ved å bruke aggregerte data får vi mer stabilitet i dataene våre, ved at de gjerne gir mindre variasjon, men dette kan skjule interessante avvik.
Sampling
Vi velger ut et subsett av dataene våre som representanter for hele settet. Her er det viktig med en rettferdig utvelgelse, og en utvelgelsesprosess som gir representative utvalg.
Dimensjonsreduksjon
For å unngå the curse of dimensionality kan vi velge å lage nye attributter som er en sammenslåing av eksisterende. Dette vil gjøre datasettet vårt mer håndterlig, men også gjøre at vi kan miste viktige detaljer.
Opprettelse av nye egenskaper
Vi kan opprette nye attributter som fanger opp mer informasjon, eller representerer den på en bedre måte. Vi kan konstruere en ny attributt k = m*n, slik at vi slipper å beregne k for hver gang vi gjør et oppslag.
Binærisering og diskretisering
Vi kan gjøre om en variabel til et kategorisk attributt, enten binært eller diskret. Dette kan gjøres både supervised (med bruk av klasser) og unsupervised (med bruk av klynger).
Transformering av attributter
Vi kan benytte en funksjon for å mappe en verdi til nye verdier. Vi kan f.eks. normalisere verdier slik at de blir like viktige i en beregning.
Likhet, ulikehet og distanse
Likhet er et numerisk mål på likheten til to dataobjekter, med høyt tall som betyr stor likhet. Ulikhet er tilsvarende et numerisk mål for ulikheten mellom to objekter.
Vi bruker som oftest et mål kalt euklidsk avstand. Vi kan også bruke manhattanavstand, som måler den "firkantede" avstanden dit vi skal (city block).
Simple matching coefficient (SMC)
Her ser vi på to sett med binære attributter. Vi sammenligner deretter om settene har den samme verdien for hvert attributt, og beregner deretter SMC = Antall like attributter / antall attributter.
Jaccard coefficient
Jaccard tar ikke hensyn til de stedene hvor begge datasettene har 0 som verdi på en attributt. Dette er nyttig i de tilfeller hvor dette ville skapt en falsk likhetsantagelse. To handlekurver som begge ikke innholder 2000 av de samme varene er neppe spesielt like, men for SMC vil antallet varer som mangler likt i begge kurvene overskygge de like elementene.
Jaccard er derfor definert som J = antall like positive attributter / antall attributter som ikke er negative matcher.
Cosinuslikhet
Her beregner vi en vektor for hver av datasettene, og regner deretter ut cosinusverdien mellom vektorene.
Korrelasjon (samvariasjon)
Måler om det er en lineær releasjon mellom to objekter. En perfekt korrelasjon er 1 eller -1.
Assosiasjonsregler
Målet med assosiasjonsregler er å finne regler som kan forutsi hvordan fremtidige sett vil se ut, basert på andre elementer i det settet.
Viktige begreper omfatter:
- Elementsett
- Dette er en samling av ett eller flere elementer.
- k-elementsett inneholder k elementer
- En transaksjon t inneholder elementsett X hvis X er et subsett av t.
- Støtteantall (support count)
- Antall forekomster av et elementsett
- Støtte (support)
- Andel av transaksjonene som inneholder et elementsett
- Frekvent elementsett
- Elementsett som har støtte som er større enn eller lik minimum støtte
For en assosiasjonsregel kan vi beregne støtte og konfidens.
Støtte er antall ganger en regel forekommer, delt på antall sett som inneholder regelens elementer.
Konfidens beregnes ved å se hvor ofte element Y forekommer i transaksjoner som inneholder X, gitt regelen X->Y. Har vi regelen {Melk, Potetgull} -> {Bleier}, så vil konfidensen være antall forekomster {Melk, Potetgull, Bleier} / antall forekomster {Melk, Potetgull}.
Oppdagelse av assosiasjonsregler
Vi har flere ulike måter å oppdage assosiasjonsregler. Den første og enkleste er brute force metoden. Vi beregner alle mulige regler, beregner støtte og konfidens, og beholder kun de som oppfyller kravene våre til minste støtte og minste konfidens. En stor utfordring med denne metoden er at den er svært beregningstung, og at de aller fleste beregninger vi gjør vil ende med å bli forkastet.
Vi kan finne nye regler ved apriori-prinsippet. Dette tilsier at hvis et elementsett er frekvent, så er også alle subsett av settet frekvent. Det følger også at et supersett ikke kan være frekvent, gitt at ett av dets subsett er ikke-frekvent.
Kompleksitet
Kompleksiteten i beregningen av assosiasjonsreglene er gitt ved en kombinasjon av
- Valg av minimum støtte
- Dimensjonaliteten til dataene
- Databasestørrelse
- Transaksjonsbredde
Størrelsen på settet av kandidatregler er gitt som |L| = k, med (2^k)-2 kandidatregler. Dette ser bort fra reglene L -> Ø og Ø -> L (hvor Ø er det tomme settet).
Klassifisering
Målet med klassifisering er å kunne forutse hvilken klasse et datasett skal få, gitt attributtene datasettet har. Typiske klassifiseringsjobber er å avgjøre om en svulst er ond- eller godartet, om en banktransaksjon er svindel, om en artikkel hører til i nyhets- eller sportsseksjonen osv.
Vi kan benytte en rekke teknikker for å klassifisere:
- Beslutningstre-metoder
- Regelbaserte metoder
- Minnebasert resonement
- Nevrale nettverk
- Naiv bayes og baysianske nettverk
- Support vector machines (SVM)
Beslutningstrær og algoritmer
Et beslutningstre er en struktur som organiserer informasjon om modellen vår i noder. Når vi ønsker å klassifisere en ny forekomst beveger vi oss nedover i treet, og tar ved hver node et valg basert på de data vi klassifiserer.
Vi kan bygge et beslutningstre ved hjelp av ulike algoritmer.
Hunt's algoritme
Hunt's algoritme er den enkleste av algoritmene som brukes til beslutningstrær. For hver node avgjør vi for de poster som tilhører noden: - Tilhører alle poster den samme klassen? Hvis ja er dette en løvnode med den klassen - Hvis ingen poster peker til noden gis den majoritetsklassen til hele datasettet - Hvis det er ulike klasser, splitt på den beste attributten, og gjenta rekursivt for alle noder
Andre algoritmer
- C4.5 -- Trenger å ha hele datasettet i minnet for å fungere, er derfor lite brukbar på store datasett.
- ID3
- CART
- SLIQ, SPRINT
Den beste splitten
For de fleste algoritmer trenger vi å definere hva som er den beste attributten å utføre en splitt på. Dette kan vi beregne ved hjelp av ulike teknikker, nevneverdig er GINI, entropi og klassifiseringsfeil (misclassification error). Målet til alle algoritmene er å finne et mål på "renheten" til en node: Hvor stor andel av tilfellene har samme klasse. Vi ønsker å oppnå så høy renhet som mulig, vi sier da at vi har høy diskrimineringsgrad.
GINI
GINI-index for en node t beregnes:
hvor P(j|t) er den relative frekvensen til klasse j i node t (andel av postene i t som tilhører klasse j). Jo lavere GINI jo bedre. Dette betyr i praksis at hvis en node har 2 klasser, med 5 forekomster av den ene og 1 av den andre, så vil den få en GINI-verdi på: 1-((5/6)^2+(1/6)^2) = 0,278
Vi kan beregne kvaliteten til en splitt av node p i k partisjoner ved å beregne den vektede GINI-indeksen for alle k partisjoner som helhet:
hvor
Med flere alternative splittinger velges den som gir størst GAINsplit:
GINI brukes som standard i CART, SLIQ og SPRINT.
Entropi
Entropi er grad av uorden på samme måte som GINI, og beregnes ved
Maksverdien er
Beregningene er, som man kan se, svært like som beregningene for GINI. For å beregne gevinst (reduksjon i entropi) fra splitt, kan vi som for GINI beregne GAINsplit:
hvor p er foreldrenoden, og i er iterasjonsvariabelen for barnenodene.
Entropi brukes som standard i ID3 og C4.5. Den har den ulempen at den foretrekker mange små partisjoner som hver for seg har høy renhet, men som ikke sammen gir et veldig riktig bilde av hvordan dataene påvirker hverandre. For å slå tilbake mot dette bruker C4.5 i tillegg en variabel som heter GAINRATIO:
med
Klassifiseringsfeil
Dette er et mål på hvor feilklassifisert en node er. Vi beregner det som
Stoppkriterie for trebygging
Et sentralt spørsmål vi kommer til er når vi skal stanse å bygge treet. Vi kan gjøre dette når det ikke lenger er mulig å utvide treet fordi all kjent informasjon er brukt opp, men dette kan være tidkrevende, og det er som vi skal se ulemper med å bygge et for nøyaktig tre.
Over- og undertilpassning (over- and underfitting)
Når man bygger et tre løper man risikoen å trene for dårlig på treningssettet, slik at man ikke blir god nok til å forutse testdata, eller at man blir så spesialisert på treningssettet at man ikke kan generalisere problemstillingen til data som er litt annerledes. Dette er kjent som henholdsvis under- og overtilpassning av modellen vår.
Undertilpassning bekjempes relativt enkelt ved å trene mer, dersom mer treningsdata er tilgjengelig. For å unngå overtilpassning må vi gå noe mer metodisk til verks. Her kan vi enten la brukeren bestemme et gitt antall iterasjoner vi skal bruke på å bygge treet, vi kan stanse når vi får en endring som er statistisk usignifikant, eller vi kan stanse når GAIN er under en gitt grenseverdi.
Modellevaluering
Når vi skal evaluere modellen vår kan vi se på nøyaktighet (accuracy). Dette er et mål på hvor mange korrekte klassifiseringer som ble gjort, altså sanne positive og sanne negative i forhold til totalt antall eksempler i settet. En utfordring med dette er dersom vi har svært ulik størrelse på noen klasser. Vi kan da oppnå nesten 100% nøyaktighet, men utelate flere klasser.
For å evaluere ytelsen til modellen kan vi bruke en av flere teknikker:
- Holdout: Vi reserverer en del av settet til testing
- Tilfeldig subsampling: Vi gjennomfører holdout flere ganger med tilfeldig utvalg
- Kryssvalidering: Vi partisjonerer data i k disjunkte sett, trener på k-1 av settene, og tester på det siste.
- Bootstrapping
- Stratified samling
Instansbaserte klassifiseringsteknikker
Instansbaserte teknikker tar utgangspunkt i at vi har lagret treningsposter, og sammenligner ukjente poster med disse for å klassifisere dem. Vi bygger altså ikke opp en modell på samme måte som når vi lager et beslutningstre eller et nevralt nettverk.
Eksempler på instansbaserte klassifiseringsteknikker er rote learner som memoriserer hele treningssettet og kun klassifiserer de poster som har en full match til en av postene i treningssettet, og nærmeste nabo klassifiserere som benytter seg av de k nærmeste punktene for å klassifisere en post.
Nærmeste nabo klassifiserere
Her benytter vi oss av et antall (k) naboer som er nærmest det punktet vi skal klassifisere. Vi må ha en metrikk for å beregne avstanden mellom punkter, og et gitt tall for antall noder vi skal bruke. Standard metrikk er euklidsk avstand.
Dersom vi velger en for liten K vil vi være sensitive mot støypunkt, mens en for stor K kan gjøre at vi ser på et alt for bredt sett av tilfeller.
Når vi behandler høydimensjonale data med nærmeste nabo klassifisering kan vi treffe på the curse of dimensionality. Dette skjer f.eks. ved at data som har mange ulike attributter kan bli klassifisert med samme likhet som data med like mange like attributter. En løsning på dette problemet er å normalisere vektorene til enhetslengder.
k-NN klassifiserere er regnet som "late klassifiserere". De bygger ikke opp en modell på forhånd, men gjør kun arbeid når det trengs, altså når vi skal klassifisere et nytt tilfelle. Dette gjør at klassifisering er en relativt dyr oppgave.
Baysianske klassifiserere
Baysianske klassifiserere benytter seg av baysianske sannsynligheter for å klassifisere en post. Gitt en variabel Y, hva er sannsynligheten for at vi skal klassifisere som X, eller mer formelt:
P(X|Y)
Dette utvides til å gjelde alle kjente attributter, og vi beregner disse sannsynlighetene på forhånd slik at de er klare til bruk.
Vi kan utvide baysianske klassifiserere ved å gjøre noen antagelser, og får dermed en naiv baysiansk klassifiserer. Her antar vi at det er uavhengighet mellom attributtene gitt klassene, og vi ser bort fra manglende verdier. Det siste er viktig da en manglende verdi vil gjøre sannsynlighetsuttrykket lik 0. Når vi kan se bort fra disse verdiene får vi en langt mer robust utregning. Ulempen er at det ikke nødvendigvis stemmer at attributtene er uavhengige.
Support vektor machines (SVM)
Målet med en support vektor machine er å finne et lineært hyperplan som separerer dataene våre. Det vil normalt være mange ulike plasseringer for hyperplanet. Den beste plasseringen er da den som har høyest margin, altså hvor avstanden til det nærmeste punktet fra planet er størst.
Hvis det er umulig å finne en lineær linje gjennom dataene kan man transformere dataene til en høyere dimensjon hvor de vil være lineært separable.
Klyngeanalyse
Målet med klyngeanalyse er å finne grupper av objekter på en slik måte at alle elementer i hver gruppe har stor likhet med hverandre, og stor ulikhet med alle andre punkter i alle andre grupper.
Det er ofte tvetydig om data tilhører en klynge eller en annen, hvor mange klynger som kan dannes fra datasettet vårt, og hvilken klynging som er den korrekte.
Vi har to hovedtyper klynginger, partisjonerte og hierarkiske klyngesett. Partisjonerte klynger er ikke-overlappende subsett av data organisert på en slik måte at hvert objekt kun finnes i ett subsett. Hierarkiske klynger er bygd opp av nøstede klynger i et hierarkisk tre, ofte representert ved et dendrogram.
Klynger kan ha en rekke egenskaper:
- Eksklusiv/Ikke eksklusiv
- Avgjør om et objekt kan tilhøre mer enn en klynge av gangen
- Fuzzy/Ikke fuzzy
- Dersom vi jobber med fuzzy klynger befinner et punkt seg i alle klynger, men med en sannsynlighet. Det er vanlig å kreve at sannsynlighetene summerer til 1.
- Delvis/Komplett klynging
- I delvise klynger blir ikke all punkter tilegnet en klynge.
- Hetrogene/Homogene klynger
Klynger har også et sett av karakteristikker:
- Godt separerte
- Punktene i en klynge er nærmere hverandre enn de er noen annen samling av punkter.
- Prototypebaserte
- En klynge kan defineres ved å velge ut et medlem som en prototype. Alle medlemmer i klyngen er da likere denne prototypen enn noen andre prototyper.
- Kontinuitetsbaserte klustere
- Dette er klynge som består av objekter som er knyttet til hverandre. De er enkle å danne fra grafbaserte data, men kan også lages ved å spesifisere en minimumsdistanse for to punkter innenfor en gruppe.
- Tetthetsbasert
- En klynge er her en gruppe med høy tetthet omgitt av punkter med en lavere tetthet.

K-means
K-means er en partisjonsbasert klyngemetode som tar utgangspunkt i et utvalg sentroider, og knytter alle andre punkter til den nærmeste sentroiden. Etter at vi har assosiert alle punkter med en sentroide beregner vi en ny sentroide i sentrum av klyngen, og gjentar prosessen. Dette gjøres til vi når en konvergens.
Det er vanlig at startsentroidene er tilfeldig valgt. Vi måler gjerne nærhet med euklidsk avstand. Konvergens kan defineres som at delta til sentroidenes nye posisjoner er mindre enn en forhåndsbestemt grense.
Evaluering av K-means-klynger
For å finne ut hvor god klyngingen vi har oppnådd er kan vi benytte en evalueringsteknikk. Den vanligste er Sum of Squared Errors (SSE). For hvert punkt finner vi avstanden til den nærmeste sentroiden. Vi summerer feilene og har da et feilmål. En ulempe med denne teknikken er at vi ved å velge like mange sentroider som det er datapunkter vil få en SSE på 0. Vi må altså balansere mellom antall klynger og lav feil. Vi kan finne et godt tall for k ved å se på grafen over SSE, plottet mot antall klynger. Der grafen har knekkpunkter ser vi at vi vil tjene mindre på å øke k. Vi velger dermed et av knekkpunktene.
Valg av startsentroider
Valget av de første sentroidene er avgjørende for hvordan K-means oppfører seg. Ettersom valget er tilfeldig kan vi ende opp med en veldig god eller veldig dårlig klynging. Dette kan vi forbedre med ulike taktikker: - Gjør klynging mange ganger med tilfeldig valg, og velg den klyngingen som har lavest SSE. - Ulempen med dette er at vi må gjøre mange kjøringer, og ikke har noen garanti for at vi bare gjør dårlige valg. - Vi kan velge startsentroidene basert på hierarkisk klynging av et sample av dataene - Vil være effektivt for små k - Velg mer enn k startsentroider tilfeldig, og velg blant disse - Her kan vi velge de sentroidene som er lengst unna hverandre - Dersom vi gjør denne utvelgelsen på et sample reduserer vi faren for å velge en outlier - Vi kan løse problemet i pre/postprosessering - Normaliser data og eliminer outliers før kjøring. - Eliminer små klynger, splitt løse klynger, slå sammen nære klynger etter kjøring. - Vi kan benytte Bisecting K-means
Bisecting K-means
Her starter vi med alle punkter i en klynge, og splitter den deretter i to ved hjelp av standard k-means. Vi gjentar dette et forhåndsbestemt antall ganger, og beholder den splitten som har den beste splitten, typisk beregnet ved SSE. De to punktene vi velger som startsentroider skal være symetrisk over linjen som deler klyngen i to. Når vi har valgt den beste splitten gjentar vi prosedyren på de nye klyngene inntil vi har k klynger.
Utfordringer med K-means
K-means er en svært effektiv algoritme, men vi har et sett begrensinger. Den fungerer dårlig på ikke-sirkulære klynger, klynger med ulik tetthet og størrelse, den håndterer outliers dårlig, og det kreves data som det er mulig å uttrykke et senter for.
Hierarkisk klynging
I hierarkisk klynging nøster vi klynger i et hierarkisk tre. Dette visualiseres som oftest som et dendrogram. Vi slipper her å ta hensyn til antall klynger. Vi kan i stedet kutte treet på et passende punkt. Svært nyttig dersom dataene vi arbeider med har en naturlig taksonomi, f.eks. biologi.
Vi har to hovedtyper hierarkisk klynging: agglomerativ og splittende (divisive). Agglomerativ klynging starter med alle punkter som individuelle klynger, og slår dem sammen til vi sitter igjen med en (eller k) klynger. Splittende (divisive) klynging starter med alle punkter i en stor klynge, og splitter til hver klynge kun har ett (eller k) punkter.
Hierarkisk klynging har et generelt minnekrav på O(n^2) pga. nærhetsmatrisen som må beregnes og holdes i minnet. Den har en tidskompleksitet på O(n^3) (Vi må utføre n steg, og gjøre et søk i matrisen for hver gang (n^2).) Vi kan med effektive datastrukturer forbedre tidskompleksiteten til O(N^2log(n)).
En ulempe med hierarkisk klynging er at når en sammenslåing først er besluttet kan den ikke gjøres om på senere.
Agglomerativ klynging
For å utføre en agglomerativ hierarkisk klynging starter vi med alle punkter som klynger. Vi finner deretter de to nærmeste klyngene og slår disse sammen. Dette gjentar vi til det kun gjenstår en klynge.
Definisjon av interklyngeavstand
Får å avgjøre avstanden mellom to klynger kan vi bruke en rekke mål:
- Min
- Den minste avstanden mellom to punkter i klyngene.
- Håndterer ikke-elliptiske former, men svak for støy og outliers.
- Max
- Den største avstanden mellom to punkter i klyngene.
- Bedre enn min til å håndtere støy og outliers, men gir ofte kuleformede klynger.
- Gruppegjennomstnitt
- Snittet av alle avstandene mellom alle punktene i klyngene.
- Er en form for kompromiss mellom Min og Max.
- Mindre følsom for støy, men er tilbøyelig til å danne kuleformede klynger.
- Det er også en svært dyr prosess å beregne alle avstander mellom alle punkter (O(m*n)).
- Sentroidedistanse
- Avstanden mellom klyngenes sentroider
- Objektivfunksjon
- Vi kan definere en objektivfunksjon som passer de dataene vi arbeider med.
Tetthetsbasert klynging med DBSCAN
DBSCAN er en tetthetsbasert algoritme som definerer tetthet som antall punkt som befinner seg innenfor en spesifisert radius Eps. Vi tilegner alle punkt en av tre kategorier:
- Kjernepunkt
- Punkt som har minst MinPts innenfor Eps inkludert seg selv.
- Grensepunkt
- Punkter som har færre enn MinPts innenfor Eps, men som selv er innenfor radius til et kjernepunkt.
- Støypunkt
- Punkt som ikke er kjerne- eller grensepunkt.
DBSCAN-algoritmen
Vi utfører DBSCAN ved å klassifisere alle punkter som enten kjerne-, grense-, eller støypunkt. Deretter eliminerer vi alle støypunkt og lager deretter grupper av kjernepunkt som er innenfor hverandres Eps. Hver separerte gruppe av kjernepunkt blir en klynge. Alle grensepunkt tilegnes til sitt kjernepunkts klynge.
Fordeler og ulemper
DBSCAN er motstandsdyktig mot støy, og håndterer irregulære klyngeformer. Den er derimot svak på varierende tettheter og høydimensjonale data. Valg av verdier for Eps og MinPts er også essensielt for god ytelse. En måte å velge Eps er å sortere alle punkt etter deres avstand til nærmeste nabo, plotte dette mot antall punkt med lik eller lavere avstand, og velge Eps ut i fra knekkpunkt i grafen.

Klyngevaliditet
Å validere klynging byr på enkelte utfordringer. Det kan tolkes subjektivt hvilken av et sett av klynginger som er bedre enn andre, og dette kan avhenge av domene. Vi har allikevel et ønske om å kunne evaluere dem, da vi ønsker å vite at vi ikke har funnet mønster i støy, eller fordi vi vil vite hvilke klyngingsalgoritmer, eller sett av klynger som er best.
Når vi gjør evalueringen kan vi gjøre den basert på ekstern index, noe som vil si at vi kjenner en ekstern faktor, f.eks. den korrekte klassifiseringen, og kan beregne entropi eller lignende. Vi kan også basere oss på intern index hvor vi kun har den informasjonen som er kjent for klyngingsalgoritmen. Da benytter vi ofte SSE. Et tredje alternativ er relativ indeks som sammenligner to forskjellige klynginger.
Siluettkoeffisient
Siluettkoeffisienten kombinerer tanker fra både kohesjon og separasjon. Kohesjon beskriver i hvor stor grad objektene i en klynge er relaterte, og beregnes ofte som summen av deres interne differanser, mens separasjon beskriver hvor stor avstand det er til andre klynger, og beregnes ofte som summen av differanser i avstand. Siluettkoeffisienten kan defineres som:
s = (b-a)/max(a,b)
hvor a = gjennomsnittlig distanse fra punkt i til punktene i klyngen til i, og b = min(gjennomsnittlig distanse fra punkt i til punkt i andre klynger). Jo nærmere 1 dette tallet kommer, jo bedre. Verdien kan ta alle tall mellom -1 og 1, hvor negative tall indikerer at det er større avstand internt i klyngen enn det er til punkter i andre klynger, noe som tyder på at klyngene våre ikke er velseparerte.