TDT4165: Programming Languages
Definitions
- The set of rules that defines the combinations of symbols that a cogized as sentences.
- Semantics
- Defines what programs do when executed.
- Syntactic sugar
- Adds a shorthand in the syntax, but does not create a new semantic.
- Compiling
- Source code is used to produce a executable binary which can be run on the target machine.
- Interpreting
- The program reads the source code when run.
- Lexical analyzer
- Reads characters and turns them into tokens ('i''f' to 'if').
- Parser
- Reads tokens and outputs a syntax tree.
Linguistic abstraction
Abstraction and addition to a language, by using already existing concepts of the language
Example: use proc to define fun
Programming paradigms
- Object oriented
- Objects encapsulate data and methods. Objects send messages and execute operations on receiving messages.
- Imperative
- The program consists of a sequence of statements which update the state of variables. Usually close to the underlying hardware.
- Declarative
- The program specifies what needs to be done and lets the language decide how it is done.
- Functional
- Programs consist of functions that compute values based on input. Pure functions are deterministic and do not have any side effects.
- Lazy execution
- Expressions are not evaluated until they are needed.
- Concurrent
- Programs are able to do several operations at the same time. That is; the order that the operations are executed in does not affect the outcome.
- Logic programming
- A program is a set of logical assertions and can be used to find out if a query is true.
Declarative programming
A program can be considered declarative if it is/have:
- immutable state
- independent of any external state
- deterministic
In other words, every time you run a declarative program with the same input (or just a declarative component) it will give you the same result (i.e. output).
Observational declarativity
A component can be seen as declarative if the definition is, even though the implementation is not
Example: A database with a declarative interface.
Higher-order programming
In higher-order programming you pass procedures/functions/objects as parameters or return values. You can also embedd them in datastuctures. (E.g. pass procedures as arguments to other procedures)
Closure = procedure value.
Four basic operations underlie all techniques in higher order programming
Procedural abstraction
Any statement can be put into a procedure. This simple snippet of code can easily be rewritten to a general procedure that would multiply the variable passed to it by two.
local B = 21 Result in
Result = B * 2
end
And here the equivialent procedure:
proc {MultiplyByTwo B ?R}
R = B * 2
end
Genericity
A generic function lets any specific entity(i.e. any operation or value) in the function body become an argument of the function. Given the above multiplying example, we can make the procedure generic(here, we also use a function, not a prodedure):
declare
fun {ApplyFunction A B F}
{F A B}
end
fun {Multiply A B}
A * B
end
{Show {ApplyFunction 21 2 Multiply}}
In ApplyFunction, we don't have any values or operations inside the function body. Instead, we extensively use the formal parameters to do our computation. We have to make the function that will act on two inputs, in this example the Multiply function. The constant
Instantiation
The abillity to return procedure values as results from a procedure call.
The act of passing procedure values to a generic function which again returns a more specific procedure which takes less/other parameters.
Given a general sorting function Sort that requires the unsorted list and a comparison function, we can instantiate this general function to sort various entities.
fun {MakeSort F}
fun {$ L}
{Sort L F}
end
end
% Dont mind this comment $
We can imagine sorting everything from numbers and letters to raccoons with this function. Calling MakeSort instantiates the specification. It returns one sorting rutine out of several possible ones, this is called the instance of the specification.
Embedding
Procedure calues can be put in data structures. An example could be the following:
fun {MultiplyByTwo A}
A * 2
end
local X in
X = [{MultiplyByTwo 1} {MultiplyByTwo 2}]
{Show X} % [2 4]
end
Relational Programming
Relational programming is an approach to programming where procedures are thought of as relations between values, and where no clear distinction between input and output is made.
The kernel language is extended with two statements:
fail, and try another alternative if it is wrong. choice statements are executed in the order they are encountered. Using this, one can state a problem, and use Oz to generate the answer.
Formal grammar
A formal grammar consists of:
- A set of terminals,
$S$ - A set of non-terminals,
$V$ - A set of rules,
$R$ - A start symbol,
$v_s$ ,$v_s \in V$
A grammar
EBNF
Extended Backus-Naur Form is a metalanguage. It is used to describe the grammar of other languages. The rules of grammar of a language can be expressed like this:
Explanation: The lefthand-side is a non-ternimal (variable) which has two production rules.
EBNF consists of terminals and variables. We can use V for variables and S for symbols.
Chomsky's hierarchy of languages
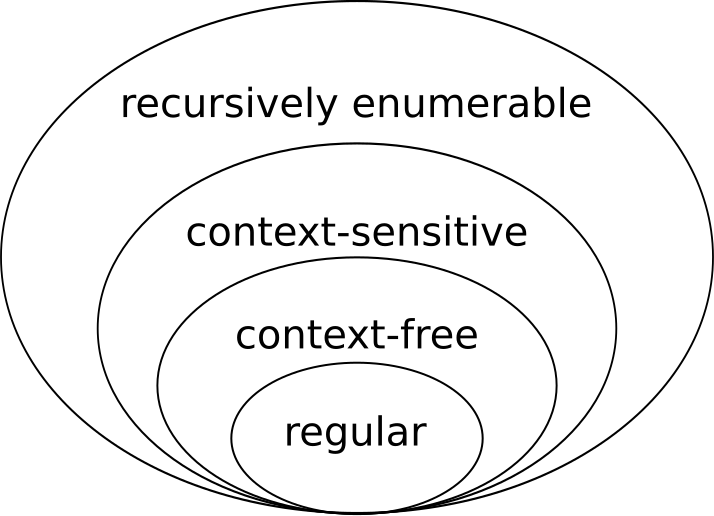
Unconstrained languages
All grammar is of the form
Context-sensitive languages
All rules are of the form
The rule only applies if the variable
Context-free languages
Generated by context-free grammar. This means that every production rule is of the form
Regular languages
A regular language is generated by regular grammar.
Derivations
A derivation is how one uses a given grammar to generate sentences from a given start symbol, showing the steps along the way. Given the grammar
we can show the derivation from
Synatax/parse trees
Each derivation gives rise to a parse tree. The parse tree is then linked to how the sentence was built from the start symbol. More often than not there are many ways to arrive at a sentence. Given a parse tree one can read the leaf nodes(terminals) and understand the sentence.
A parse tree can be used to; interpret a program(in interpreted languages), generate code(in compiled languages) or optimize intermediate code(both comiled and interperted).
Ambiguity
A grammar is abiguous if a sentence can be parsed in more than one way. This means that the sentence has more than one parse tree. Programming languages cannot be ambiguous since that would give rise to several different meanings of the same sentence.
There are several ways to avoid ambiguity in grammars: Parantheses, precedence and associativity.
Scope
The scope of a name binding is where in the program the name binding is valid. (E.g where it can be used). A name binding is a association between a identifier and variable/value.
Lexical scope
The following example demonstrates the difference between lexical(static) and dynamic scope. What is the resulting output of the program?
local P Q in %
proc {Q X} {Browse static(X)} end
proc {P X} {Q X} end
local Q in
proc {Q X} {Browse dynamic(X)} end
{P hello}
end
end
Here, we have created the identifier 'Q' twice. It refers to different procedures, browsing either static(hello) or dynamic(hello). In static scoping, we can find the value of an identifier simply by looking at its scope. This results in printing 'static(X)' in the program above. Note: Oz has static scoping.
Dynamic scope
Dynamic scoping keeps the scope of the caller when calling a function. Thus, the program above would result in printing 'dynamic(X)'. This is because it created a new identifier 'Q', bound this to a procedure, and then called the procedure P.
Syntax, Semantics and DSKL
Syntax & Semantics
The syntax is a set of rules, principles and processes that govern the structure of sentences in a language. There are three levels of syntax:
- The Lexical Level
- The Syntactic (Grammar) Level
- The Semantic Level
We regard words on the Lexical Level, how characters form tokens. These tokens can be keywords, operators, identifiers ++. The lexical syntax can be expressed in a formal regular grammar. We use regular expressions(from regular grammar) to define lexemes. Note: A lexeme is the sequence of characters that make up a language element, while a token is a structured representation of that element that can be used by the compiler or interpreter.
The Syntactic Level determines how tokens form phrases. Phrases are expressed in a context-free grammar.
There also exists the context level, which determines what objects and variables refer to.
The Semantic Level gives rise to the meaning of the program within the language it is written in.
Syntactic Sugar
Syntactic sugar are abbreviations of longer and often less readable code. It does not introduce any new functionality. In oz we can declare variables in a number of ways;
local X in
local Y in
# Code
end
end
Or we can do the cleaner
local X Y in
# Code
end
Where the latter is syntactic sugar for the former.
Linguistic abstractions
Linguistic abstractions are another way to express functionality that is already in the language. A great example of this is the following:
if <expression> then
# Code
end
is actually the following code in disguise
if <expression> then
# Code
else
skip
end
Here we seem to have introduced a new kind of if-statement, namely the if-statement without an 'else' clause. However, this is not the case, as the former code is really the latter.
DSKL (Declarative Sequential Kernel Language)
What is a Kernel Language?: A 'Kernel Language' (or a Core Language) refers to the subset of a language for which everything else is Syntactic Sugar
DSKL Generally referes to the Core Language of Oz
Abstract Kernel Language Machine
The abstract machine(or virtual machine(VM)) is a model of computation, explaining the execution of programs in a high level way. We can easily expand the VM to support several programming constructs(?) such as error handling and parallelism.
Components of the VM
The VM consists of two parts: The Semantic stack(SS) and a single assigment store(SAS).
The stack contains semantic statements. Each semantic statement is a pair of a parsed statement and an environment. The statement is a small piece of code to be evaluated. The environment is a mapping from identifiers in the code to variables in the store.
Execution on the VM
The program is executed on the VM. This execution is roughly done by looking at the topmost statement in the SS, then manipulating the SAS accordingly, followed by the next statement in the SS. Here is an example where we want to unify two unbound variables follow: Before the execution we have:
Single Assignment Store(SAS)
The sas consists only of declarative variables, that is variables that stays bound throughout the computation, and is indistinguishable from their value. This means that
Variables
When writing
local X Y Z in
X = "Ola"
Y = person(name:X age:Z)
end
In the above code, X is a bound variable. Y is a partially bound variable because the data structure contains an unbound variable(Z). And Z is an unbound variable. The corresponding store could look like
Dataflow Variables
In our declarative programming model, creating a variable and binding it are done separately(this is why we can have unbound variables). Declarative variables that cause the program to wait until they are bound are dataflow variables. This is useful when doing concurrent programming(which we will get back to later).
Tail Recursion
When a function calls itself(or another function for that matter) at the end of the function, it is called tail recursion. Whenever a program calls itself, a lot of data are being pushed on the stack(program counter, environment, return address). The stack might fill up if the recursion goes to deep, resulting in a program crash. Tail recursion avoids this problem:
fun {Member Xs Y}
case Xs of nil then
false
[] Head|Tail then
if Head == Y then
true
else
{Member Tail Y}
end
end
end
In the program above we see that the last thing our function does is to call itself. The other variables(Head and Tail in this example) will never be needed again after the recursive call to Position. Hence the abstract machine does not need to push the environment on the stack. Indeed, does not need the stack at all because the program might as well be done iteratively. We can also express this in a formal grammar:
Since the last
Exceptions
To implement exceptions, we expand extend the kernel language both semantically and syntactically.
Syntactic extension
The statement gets two new rules:
The try statement contains two statements, namely one in try and one in catch. The two statements are pushed on the stack, firstly the statement inside catch, then the statemenet inside try. If something fails in the try statement, the VM can just pop everything of the stack until it reaches a catch, which will resolve the problem.
The raise statement will pop a semantic statement from the stack, if the statement is a catch statement, push that semantic statement onto the stack. If it isn't a catch statement, repeat.
Oz
Functions and procedures
Functions returns a value, procedures do not. That means that procedures do not care about the number of input, nor the number of output values.
Procedures are a basic type of Oz, which functions are based upon.
proc {NameOfProcedure V1 ?V2} % Declare a procedure
% Do something
V2 = v1
end
% The question mark in front of the output argument V2 is just to make the definition easier to read, and has no effect on execution
fun {NameOfFunction V1 V2}
% Do something with V2 or whatever you want, I don't really care cause' this is an example
V1 % function returns V1
end
% Call them
local
X = 2
Y = 1
Z
in
{NameOfProcedure X Z}
{Browse Z} % returns 2, as the procedure binds V2 to the value of V1
Z = {NameOfFunction Y X}
{Browse Z} % returns 1, as the function returns V1 which is Y
end
The function statement is syntactic sugar. Let's translate a function to a procedure (page. 84):
fun {F X1 .. XN] <statement> <expression> end
proc{F X1 ... XN ?R } <statement> R = <expression> end
We see that the function lets you return a value, which is the same as giving a procedure an argument and binding it to the return expression.
On the semantic stack, a procedure is stored as a procedure value,
Higher order functions
Dataflow
Declarative variables that cause the program to wait until they are bound are called dataflow variables. In the declarative model, creating a variable and binding it are done separately.
Declarativity
Variables in Oz are declarative, meaning they cannot be reassigned another value after the initial binding.
declare X in
X = hello
X = world % This will fail
Records
Records are a basic type of Oz. They are of the form
X = person(name:"George" age:25)
much like dictionaries in Python (associated list), and contains a tuple of literals. Operations:
X = person(name:"George" age:25)
{Arity X} % returns [name age]
{Label X} % returns person
X.age % returns 25
Touples
A touple is a data type that contains several literals. They are of the form
(name:"George" age:25)
Literals
A literal is an atom or a name. This could be seen as
25
in the touple above.
Lists
List are nested records.
% Equivalent:
List1 = '|'(1 '|'(2 '|'(3 nil)))
List2 = [1 2 3]
List3 = [1|[2|[3|nil]]]
Difference lists
A difference list is a pair (tuple) of two ordinary lists, where each might have an unbound tail. It must be possible to get the second list from the first list by removing zero or more elements from the front of the first list. Example:
nil#nil % Represents the empty list
[a]#[a] % Also represents the empty list
(a|b|c|X)#X % Represents [a b c]
[a b c d]#[d] % Also represents [a b c]
Concurrency
In Oz, each thread is data-flow, and blocks on data dependency. We'll take a look at this code.
declare X1 X2 in
thread
local Y1 Y2 in
{Browse [Y1#Y2]}
Y1 = X1 + 1
Y2 = X2 + 2
end
end
Notice that Y1 and Y2 are partially bound variables that are dependent on X1 and X2. Since the Browse procedure spawns a new thread that peeks on Y1 and Y2, we can observe Y1 and Y2 appear unbound. The thread is suspended, and initially dependent on X1.
If we were to gradually bind the variables X1 and X2, we would notice our thread resuming and suspending.
X1 = 3
%The thread will start calculating Y1. It will then suspend while waiting for X2
X2 = 4
%The thread will start calculating Y2, and thus terminate
We also notice that the reason that the thread was executed concurrently in correct order is because of these data dependencies.
Futures and the ByNeed operation
Futures are used for lazy / demand driven computations. Futures are created as partially bound variables
F = !!X %Double negation used to avoid direct unification
ByNeed can be used to introduce lazy procedures, by taking a one argument procedure and returning the future F of it.
declare
F
proc {BigFancyProcedure X} X = 42 end
{ByNeed BigFancyProcedure F}
The future F will now ensure that BigFancyProcedure will not compute and bind X until F is attempted accessed. Wait is a way to access F for the sole reason to trigger F's procedure
{Browse F} % Browser will at first show F<Future>
{Wait F}
% some time passes, and the Browser will show the value of X
Lazy evaluation
<TBD>
Streams
A stream in Oz is a list with a unbound variable as its last element. This variable can again be a stream. This means a stream in theory can be infinite.
Explicit state
State in Oz is implemented by the use of cells. To create a variable that you can assign to multiple times
A = {NewCell 0} % Creates a new cell with initial value of 0
To assign something to the cell A, use the following syntax:
A := 10 % Assigns 10 to the cell A
To access the value of the cell do:
@A
A full example using cells to sum the contents of a list
fun {SumList List} Sum in
% Creates a new cell
Sum = {NewCell 0}
% Iterates over each element in the list
for Element in List do
Sum := @Sum + Element
end
@Sum
end
Encapsulation
<TBD>
Inheritance
<TBD>
Pattern Matching
case List of <pattern> then
% Do something
[] <otherPattern> then
% Do something else
else then
% Whoo, something completely weird and CRAZY
end
Notice here that the use of [] is syntactic sugar, and in the Core Language of Oz this would be represented:
case Xs of <pattern> then
% Do something
else then
case Xs of <otherPattern> then
%Do something else
else then
% Whoo, something completely weird and CRAZY
end
end
When writing patterns as part of pattern matching, Oz will create variables in the local environment/scope that correspond to different parts of the pattern.
case List of Head|Tail then
% Let's say the List is [1 [2 [3]]]
% Now Head is 1, and Tail is [2 [3]]
Non-determinism
<TBD>
Scala
We are only covering concurrency and actors in scala, so this is what the section will focus on.
Threads
Threads are separate running computations in a program. A thread can be in one of several states, among them being:
- New
- A Thread object is automatically in this state after it is created.
- Runnable
- A Thread is Runnable when the Thread object starts executing.
- Waiting
- Waiting threads notify the OS that thay are waiting for some condition and cease spending CPU cycles, instead of repetitively checking that condition.
- Terminated
- After a Thread is done executing, it goes into this state. It cannot execute any more.
Prolog
Church Encoding
In Church Encoding, we have Church Numerals, which are defined by Lambda Calculus (don't look into it too much). Essentially, 0 is defined as the first numeral, and the successor to a numeral is also a numeral.
numeral(0) //0 is a numeral
numeral(succ(X)) :- numeral(X)
If we wanted to represent 4, we would write either of these
succ(succ(succ(succ(0))))
succ(3)
However, if we would query with '?- numeral()' to check if these representational were numerals, TRUE would only hold for the first case, because we only know that 0 and it's successors are numerals. 3 is not implicitly defined as a numeral.
There are 6 functions that apply to Church numerals; succession, predecession, addition, subtraction (monus), multiplication, and exponentiation
<TBD>