# Hva er Algoritmer? __En uformell definisjon__: En algoritme er en hvilket som helst __tydelig definert fremgangsmåte__ som kan ta en verdi (eller en mengde verdier) som __input__ og gir en verdi (eller en mengde verdier) som __output__. __Beskrivelse av løsning__: Det finnes ingen verdensomspennende standard for å beskrive en algoritme. Du kan beskrive den med naturlig språk, som et dataprogram eller til og med ved hjelp av å tegne maskinvare (hardware) som løser problemet. Det eneste kravet er at du er presis når du beskriver. __Instanser__: Hver samling av input-verdier til et slikt problem kalles en __instans__. For eksempel kan man i en instans av problemet over ha input-verdier som er et veikart over Trondheim, og de to punktene kan være to geografiske punkter som tilsvarer NTNU Gløshaugen og NTNU Dragvoll. __Riktig eller uriktig?__: En algoritme kan være enten __riktig__ eller __uriktig__. Dersom en algoritme er _riktig_, vil den for alle tenkbare instanser (innenfor området vi har bestemt) gi riktig output; f.eks. er det bare å forvente at en sorteringsalgoritme ikke vil ha problem med å sortere alle mulige samlinger av positive heltall. Dersom den er _uriktig_, vil den ikke gjøre det. F.eks. kan du ha funnet på en algoritme som løser alle sorteringsproblemer ved å vende rekken av tall du har fått baklengs. Dette vil for noen instanser gi riktig output, men bare for en brøkdel av alle mulige instanser. # Kjøretid Kjøretiden til en algoritme er et mål på hvor effektiv en algoritme er og uten tvil det viktigste. ## Om kjøretider __Hvorfor trenger vi kjøretid?:__ I en verden der datamaskiner var uendelig raske og du hadde uendelig med tilgjengelig lagringsplass, kunne du brukt en hvilken som helst _riktig_ algoritme for å løse et problem – uansett hvor lite gjennomtenkt den måtte være. Men, som du sikkert har merket, er vi ikke i denne verdenen. Derfor har vi kjøretider. __Forklaring av kjøretid__: En kjøretid beskriver det asymptotiske forholdet mellom størrelsen på problemet og hvor lang tid det vil ta å løse det. ## Noen vanlige kjøretider || __Kompleksitet__ || __Navn__ || __Type__ || || $\Theta(n!)$ || Factorial || Generell || || $\Omega(k^n)$ || Eksponensiell || Generell || || $O(n^k)$ || Polynomisk || Generell || || $\Theta(n^3)$ || Kubisk || Tilfelle av polynomisk || || $\Theta(n^2)$ || Kvadratisk || Tilfelle av polynomisk || || $\Theta(n \lg n)$ || Loglineær || Kombinasjon av lineær og logaritmisk || || $\Theta(n)$ || Lineær || Generell || || $\Theta(\lg n)$ || Logaritmisk || Generell || || $\Theta(1)$ || Konstant || Generell || # Kjøretidsberegning Rekursjon er en problemløsningsmetodikk som baserer seg på at løsningen på et problem er satt sammen av løsningene til mindre instanser av samme problem. Denne teknikken kommer til å gå igjen i mange av algoritmene i pensum. Et av de aller vanligste eksemplene på rekursivitet er Fibonaccitallene, definert som: $$F(n) = F(n-1) + F(n-2)\\ F(0) = 0, F(1) = 1$$ Fibonaccitall $n$ er altså definert som summen av de to foregående Fibonaccitallene. Gode eksempler på rekursive algoritmer er Merge og Quick Sort og binærsøk. Vi finner også ofte rekursive løsninger ved bruk av dynamisk programmering. ## Masterteoremet Masterteoremet er en kokebokløsning for å finne kjøretiden til (mange) rekurrenser på formen $$ T(n) = aT(^n/_b) + f(n) \\ a \ge 1, b \gt 1 $$ Denne typen rekurrenser oppstår gjerne i sammenheng med splitt-og-hersk algoritmer, f.eks. Merge sort. Problemet deles opp i $a$ deler av størrelse $^n/_b$, med f(n) arbeid for å gjøre selve oppdelinga, og å sette sammen resultatet av rekursive kall etter at disse er ferdige. I eksempelet med Merge sort, er f(n) arbeidet med å splitte lista i to underlister, og å flette sammen de to sorterte listene etter at de rekursive kallene er ferdige. Det å splitte skjer i konstant tid $\Theta(1)$, mens det å flette sammen tar lineær tid $\Theta(n)$. Vi kan altså sette $f(n) = n$. Siden vi til enhver tid deler listen opp i to deler, hver del $^n/_2$ er henholdsvis $a=2$ og $b=2$. For Merge sort har vi altså: $$ T(n) = 2T(^n/_2) + n $$ Dersom vi ikke allerede visste kjøretiden til Merge sort, kunne vi funnet den ved å løse denne rekurrensen. Å løse rekurrensen kunne vi så brukt Masterteoremet til. Fremgangsmåten for Masterteoremet er som følger: 1. Identifiser $a, b, f(n)$ 2. Regn ut $\log_b a$ 3. Konsulter tabellen under Tabell over de tre tilfellene av Masterteoremet: || **Tilfelle** || **Krav** || **Løsning** || || 1 || $f(n)\in O(n^{\log_b a-\epsilon})$ || $T(n) \in \Theta(n^{\log_b a})$ || || 2 || $f(n)\in \Theta(n^{\log_b a} \log^k n)$ || $T(n) \in \Theta(n^{\log_b a}\log^{k+1} n)$ || || 3 || $f(n)\in \Omega(n^{\log_b a+\epsilon})$ || $T(n) \in \Theta(f(n))$ || $\epsilon > 0$ Vi fortsetter eksempelet med Merge sort. Vi har funnet $a=2, b=2, f(n)=n$, da må $\log_b a = \log_2 2 = 1$. Vi har altså tilfelle 2, $f(n) \in \Theta(n^1)$, med løsning $T(n) \in \Theta(n\lg n)$. ### Eksempel Enda et eksempel, hentet fra kontinuasjonseksamen 2009: Løs følgende rekurrens. Oppgi svaret i asymptotisk notasjon. Begrunn svaret kort. $$ T(n) = 2T(^n/_3) + ^1/_n $$ Vi har $a = 2, b = 3, f(n) = n^{-1}$. Det gir $\log_b a = \log_3 2 \approx 0.63$. Siden $f(n) = n^{-1}$ er $O(n^{.63})$, har vi tilfelle 1 og løsningen $T(n) \in \Theta(n^{.63})$. # Grunnleggende datastrukturer Faget går gjennom og nyttiggjør seg av mange ulike datastrukturer i sammenheng med ulike problemstillinger, og det kan derfor være greit å ha oversikt over de viktigste. 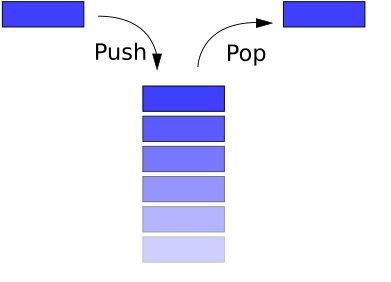## Stacks and Queues (Dynamic Sets) Stakker og køer er dynamiske sett med 2 viktige metoder, PUSH og POP, som betyr hhv. å legge til og fjerne et element. Merk at et POP-kall og et DELETE-kall er det samme. 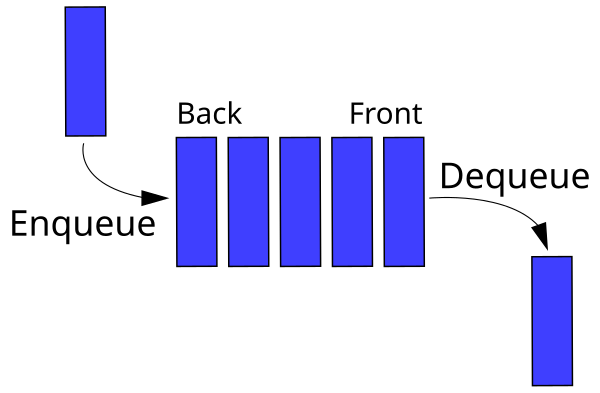### Queue En queue er en FIFO (First In First Out) struktur. Dette vil si at et POP-kall til køen returnerer elementet som __først__ ble satt inn.  ### Stack En stakk er LIFO (Last In First Out) struktur. Et POP-kall til stakken returnerer elementet som __sist__ ble satt inn.  ## Lenkede lister  _[Singly linked list (Public Domain, Lindisi)](https://en.wikipedia.org/wiki/Singly_linked_list#mediaviewer/File:Singly-linked-list.svg)_ En lenket liste er en enkel lineær datastruktur som representerer elementer i sekvens. Hvert element peker på det neste (se figur over). I en dobbelt-lenket liste peker det også på det forrige elementet. ### Implementere lenkede lister I OOP (Object-Oriented Programming) benytter en objekter og pekere. Python-kode for en lenket liste: class Node: def __init__(self, key): self.key = key self.prev = None self.next = None def set_pointers(prev, next): self.prev = prev self.next = next n1 = Node(9) n2 = Node(4) n3 = Node(1) n4 = Node(5) n1.set_pointers(None, n2) n2.set_pointers(n1, n3) n3.set_pointers(n2, n4) n4.set_pointers(n3, None) I språk som ikke støtter objekter eller pekere kan en bruke arrays. L holder her indeksen til det første elementet. L = 4 0 1 2 3 4 5 6 -------------------------- NEXT = [/, 2, 6, /, 1, /, /] KEY = [/, 4, 1, /, 9, /, 5] PREV = [/, 4, 1, /, /, /, 3] Dette kan også gjøres komprimeres til et enkelt array, der hver node er 3 etterfølgende verdier, (prev, key, next). L = 1 0 1 2 3 4 5 6 7 8 9 10 11 ----------------------------------------- LIST = [/, 9, 4, 1, 4, 7, 4, 1, 10, 7, 5, /] Klarer du å se at alle de lenkede listene er identiske? ### Kjøretider || **Handling** || **Kjøretid** || || Innsetting på starten || O(1) || || Innsetting på slutten || O(n) || || Oppslag || O(n) || || Slette element || oppslagstid + O(1) || # Sortering Stort sett kategoriserer vi sorteringsalgoritmer inn i to grupper; sammenligningsbaserte og distribuerte/ikke-sammenlignin gsbaserte. ## Stabilitet En sorteringsalgoritme kan sies å være stabil dersom rekkefølgen av like elementer i listen som skal sorteres blir bevart i løpet av algoritmen. Altså; dersom vi har listen: $$[B_1, C_1, C_2, A_1]$$ og sorterer den med en eller annen algoritme, og de to like elementene står i samme rekkefølge etter sorteringen, har vi en stabil sorteringsalgoritme. $$[A_1, B_1, C_1, C_2]$$ Altså har vi at selv om _verdien_ til $C_1$ og $C_2$ er den samme så blir $C_1$ sortert før $C_2$. ## Sammenligningsbaserte sorteringsalgoritmer Alle sorteringsalgoritmer som baserer seg på å sammenligne to elementer for å avgjøre hvilket av de to som skal komme først i en sekvens, kaller vi sammenligningsbasert. Det er vist at $\Omega(n\lg n)$ er en nedre grense for antall sammenligninger en sammenligningsbasert sorteringsalgoritme må gjøre. Med andre ord, det er umulig å lage en sammenligningsbasert sorteringsalgoritme som har bedre best-case kjøretid enn $O(n\lg n)$. ### Merge sort Merge sort er en splitt-og-hersk algoritme. || __Best Case__ || __Average Case__ || __Worst Case__ || __Stabil__ || __Space__ || || $O(n\log n)$ || $O(n\log n)$ || $O(n\log n)$ || Ja || $O(n)$ || 1. Todel listen rekursivt til hver liste inneholder 1 element. (En liste med ett element er per definisjon sortert) 2. Flett sammen underlistene. I praksis blir dette gjerne implementert rekursivt. Merge funksjonen kjører i lineær tid. For å analysere kjøretiden til Merge sort kan vi sette opp følgende rekurrens: $$T(n) = 2T(n/2) + n$$ Altså 2 ganger tiden det tar å sortere en liste av lengde $^n/_2$ pluss tiden det tar å flette de to listene. Se [Masterteoremet](#masterteoremet) for hvordan vi kan løse denne rekurrensen og finne kjøretiden $O(n\log n)$. De fleste implementasjoner av Merge sort er stabile. På grunn av at algoritmen hele tiden lager nye underlister, trenger den $O(n)$ ekstra plass i minnet. ### Quicksort (Randomized) Quicksort er en splitt-og-hersk algoritme. || __Best Case__ || __Average Case__ || __Worst Case__ || __Stabil__ || __Space__ || || $O(n\log n)$ || $O(n\log n)$ || $O(n^2)$ || Nei || $O(\log n)$ || Konseptet med et __pivot__-element står sentralt i quicksort. For hver iterasjon velger en seg et pivot-element og sorterer resten av elementene basert på om de er større eller lavere enn pivot-elementet. Hvis pivot-elementet velges tilfeldig kalles algoritmen Randomized-Quicksort. 1. Velg et pivot-element. 2. Sorter resten av elementene i 2 del-lister utifra om de er større eller mindre enn pivot. 3. Sorter de 2 del-listene rekursivt til de bare inneholder 1 element. Kjøretidsanalysen av Quicksort blir noe vanskeligere enn for Merge sort, ettersom størrelsen på listene som sorteres rekursivt vil avhenge av hvilken pivot vi velger. Det å velge en god pivot er en kunst i seg selv. Den naïve fremgangsmåten med å slavisk velge det første elementet, kan lett utnyttes av en adversary, ved å gi en liste som er omvendt sortert som input. I dette tilfellet vil kjøretiden bli $n^2$. Vi kan motvirke dette ved å velge en tilfeldig pivot i stedet. ### Heapsort Heapsort bruker trestrukturen [heap](#heaps) til å sortere. || __BC__ || __AC__ || __WC__ || __SC__ || __Stable__ || || $\Omega(n\log n)$ || $\Theta(n \log n)$ || $O(n \log n)$ || $O(1)$ || Nei || ### Bubblesort Traverserer listen, sammenligner to elementer og bytter plass på dem hvis nødvendig. || __BC__ || __AC__ || __WC__ || __SC__ || __Stable__ || || $\Omega(n)$ || $\Theta(n^2)$ || $O(n^2)$ || $O(1)$ || Ja || ### Insertion Sort Setter inn element _i_ på rett plass i den allerede sorterte lista av _i_-1 elementer. || __BC__ || __AC__ || __WC__ || __SC__ || __Stable__ || || $\Omega(n)$ || $\Theta(n^2)$ || $O(n^2)$ || $O(1)$ || Ja || ### Selection sort Veldig dårlig sorteringsalgoritme, søker gjennom hele lista og finner det minste elementet hver gang. || __BC__ || __AC__ || __WC__ || __SC__ || __Stable__ || || $\Omega(n^2)$ || $\Theta(n^2)$ || $O(n^2)$ || $O(1)$ || Nei || ## Ikke-sammenligningsbaserte sorteringsalgoritmer Sorteringsalgoritmer som ikke er sammenligningsbaserte er ikke begrenset av $O(n\lg n)$ som nedre grense for kjøretid. ### Counting sort Denne algoritmen antar at input er heltall fra et begrenset intervall, k. Counting sort teller hvor mange elementer som er lavere eller lik det elementet som skal sorteres, og putter det på riktig plass i lista. Dette er en stabil søkealgoritme. || __BC__ || __AC__ || __WC__ || __SC__ || __Stable__ || || $\Omega(n + k)$ || $\Theta(n + k)$ || $O(n + k)$ || $O(k)$ || Ja || Dersom $ k = O(n)$ , får vi kjøretid $ \Theta(n)$ ### Radix sort Radix sort antar at input er _n_ elementer med _d_ siffer, der hvert siffer kan ha opp til _k_ forskjellige verdier. Algoritmen ser som regel på det minst signifikante sifferet, sorterer med hensyn på dette sifferet, og gjentar så med det nest minst signifikante sifferet, osv. Om sortseringen på hvert siffer er basert på en algoritme som sorterer stabilt på $\Theta(n+k)$ (feks counting sort), vil hele algoritmen bruke $\Theta(d(n+k))$ tid. || __BC__ || __AC__ || __WC__ || __SC__ || __Stable__ || || $\Omega(d(n + k))$ || $\Theta(d(n + k))$ || $O(d(n + k))$ || $O(n+k)$ || Ja* || ### Bucket sort Bucket sort antar at inputen er generert fra en tilfeldig (random) prossess som fordeler elementene uniformt og uavhengig over et intervall. Bucket sort deler intervallet inn i _n_ like store "bøtter" (intervaller), og fordeler så de _n_ inputtallene i bøttene. Hver bøtte sorteres så for seg vet å bruke en sorteringsalgoritme, bucket sort, insertion sort eller en annen algoritme. || __BC__ || __AC__ || __WC__ || __SC__ || __Stable__ || || $\Omega(n + k)$ || $\Theta(n + k)$ || $O(n^2)$ || $O(n)$ || Ja || ## Søking Sortering og søking er to problemstillinger som går igjen enten som problem i seg selv, eller som underproblem. Med sortering mener vi det å arrangere en mengde med objekter i en spesifikk rekkefølge. Med søking mener vi det å finne ett spesifikt objekt i en mengde objekter. Det å finne et spesifikt element i en datastruktur er et utbredt problem. I en liste av tall kan vi f.eks. lete etter medianen eller bare et bestemt tall. I en graf kan vi f.eks. lete etter en måte å komme oss fra ett element til et annet. Søkealgoritmer for grafer (DFS og BFS) står under [Graf-algoritmer](#grafer-og-grafalgoritmer). For å søke i lister, har vi primært to fremgangsmåter; brute force og binærsøk. ### Brute force Denne fremgangsmåten er ganske selvforklarende. Gå gjennom lista (sortert eller ikke) fra begynnelse til slutt og sammenlign hvert element mot elementet du ønsker å finne. Med $n$ elementer i lista blir kjøretiden $O(n)$ ### Binærsøk Dersom vi vet at lista vi skal søke i er sortert, kan vi bruke en litt annen strategi. Si at vi leter etter en verdi $a$ i en sortert liste $L$. Vi begynner med å finne det midterste elementet i $L$ og sjekker om det er lik elementet vi leter etter. Dersom ja, returner indeksen, dersom ikke, avgjør om elementet i leter etter er større enn eller mindre enn det midterste, og gjenta deretter prosedyren i den underlista der elementet må være, dersom det i det hele tatt ligger i lista. Siden vi for hver iterasjon todeler listen, og kan forkaste halvparten får vi følgende kjøretider: || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(1)$ || $O(\log n)$ || $O(\log n)$ || ## Kompleksitet og Stabilitet for Sortering- og Søkealgoritmer - $n$ er antallet elementer som skal jobbes med. - $k$ er den høyeste verdien tallene kan ha. - $d$ er maks antall siffer et tall kan ha. - __BC__ == Best Case - __AC__ == Average Case - __WC__ == Worst Case - __SC__ == Space Complexity Worst Case || __Algoritme__ || __BC__ || __AC__ || __WC__ || __SC__ || __Stable__ || || Merge || $\Omega(n\log n)$ || $\Theta(n \log n)$ || $O(n^2)$ || $O(\log n)$ || Ja || || R-Quick || $\Omega(n\log n)$ || $\Theta(n \log n)$ || $O(n \log n)$ || $O(n)$ || Nei || || Heap || $\Omega(n\log n)$ || $\Theta(n \log n)$ || $O(n \log n)$ || $O(1)$ || Nei || || Bubble || $\Omega(n)$ || $\Theta(n^2)$ || $O(n^2)$ || $O(1)$ || Ja || || Insertion|| $\Omega(n)$ || $\Theta(n^2)$ || $O(n^2)$ || $O(1)$ || Ja || || Selection|| $\Omega(n^2)$ || $\Theta(n^2)$ || $O(n^2)$ || $O(1)$ || Nei || || Bucket || $\Omega(n + k)$ || $\Theta(n + k)$ || $O(n^2)$ || $O(n)$ || Ja || || Counting || $\Omega(n + k)$ || $\Theta(n + k)$ || $O(n + k)$ || $O(k)$ || Ja || || Radix || $\Omega(d(n + k))$|| $\Theta(d(n + k))$ || $O(d(n + k))$ || $O(n+k)$ || Ja* || || Select || $O(n)$ || $O(n)$ || $O(n)$ || NA || NA || || R-Select || $O(n)$ || $O(n)$ || $O(n^2)$ || NA || NA || * Radix sort krever en stabil subrutine for selv å være stabil. # Dynamisk programmering Dynamisk programmering brukes når delproblemene overlapper. Hvis en på visse problemer bruker standard splitt-og-hersk vil en løse samme problem flere ganger og dermed gjøre unødvendig arbeid. Dynamisk programmering løser delproblemet en gang og lagrer svaret til bruk i resten av problemet. For at vi skal kunne gjør dette må problemet ha __optimal substruktur__. Vanlige problemstillinger som kan løses vha DP - Longest common subsequence - Rod cutting ## Optimal substrukur Et problem har optimal substruktur hvis en optimal løsning inneholder optimale løsninger på delproblemer. Merk at størrelsen på delproblemene ikke er spesifisert, en kan altså ikke redusere de til deres enkleste komponenter som i [merge sort](#merge-sort). ## Longest common subsequence Løses med dynamisk programmering fra bunnen og opp, ved å se på det siste elementet i hver liste. ## Rod-cutting Gitt en stav med lengde n, og en liste med priser for alle lengder kortere enn n. Avgjør hva maksimal fortjeneste blir ved å kutte den opp og selge den. # Grådige algoritmer Noen ganger er dynamisk programmering overkill. Grådige algoritmer velger den løsningen som ser best ut akkurat nå, og går videre. Dette vil føre til den optimale løsningen hvis problemet har __Greedy-choice property__. I tillegg må problemet ha __optimal substruktur__. Vanlige problemer som kan løses av GA er: - Aktivitetsutvalg - Huffman-kode ## Greedy-choice property Vi kan ta et valg som virker best i det øyeblikk og løse subproblemene som dukker opp senere. Valget gjort av grådige valg kan ikke være avh. av fremtidige valg/alle løsningene til problemet så langt ## Aktivitetsutvalg Velg så mange ikke-overlappende aktiviteter som mulig. Anta at de er sortert etter sluttid og bruk en grådig algoritme til å velge dem. ## Huffmans algoritme Huffmans algoritme er en grådig algoritme med formål å minimere lagringsplassen til en kjent sekvens med symboler. Hvert symbol kan representeres av en binær kode av lik lengde. Ved å telle antall hendelser av hvert symbol og bygge et binærtre basert på frekvensene kan man redusere antall bits som trengs til å lagre sekvensen med 20%-90%. Huffman utføres ved å alltid legge sammen de nodene med minst verdi, også bruke summen av verdiene som en ny node. Ved å la en gren til venstre være $0$ og en gren til høyre være $1$ vil alle symbolene kunne representeres med en unik binær kode. De symbolene som brukes hyppigst vil få en kortere kode en de som brukes sjeldnere. || __Best case__ || __Average case__ || __Worst case__ || || $O(n \lg n)$ || $O(n \lg n)$ || $O(n \lg n)$ || En verson av huffman kan i praksis se slik ut:  # Grafer og Trær ## Grafer En graf modellerer parvise __relasjoner__ mellom objekter. En graf er en slags helhetlig oversikt over mange små enkelte relasjoner. En graf består av __noder__ (vertices) og __kanter__ (edges). Fordi mange problemer kan modelleres som grafer er denne datastrukturen noe av det viktigste i faget. Matematisk betegner vi ofte nodesettet V for vertices og kantsettet E for edges. En graf blir dermed G = (V, E) En graf kan være både __rettet__ (directed) og __urettet__ (undirected). I en urettet graf er det en kant (v, u) hvis det er en kant (u, v). I en rettet graf er dette ikke nødvendigvis sant. En graf kan se ut f.eks. 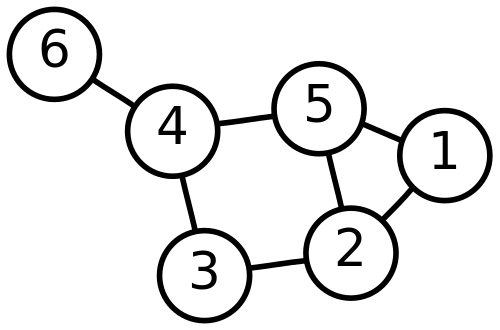som dette:  ### Trær Et tre er en begrenset gruppe type graf. Trær har retning (parent / child forhold) og inneholder ikke sykler. Trær kan også defineres som grafer der, for hvert par noder $u,v \in V$, så eksisterer det én(og bare en) enkel sti mellom $u$ og $v$. Hvis hver node i et tre også har kun en forelder så har vi en DAG (Directed Acyclic Graph). #### Binærtrær Et tre er et binærtre hvis hver node har maks 2 barn. __Fullt binærtre__: Alle interne har to barn __Balansert binærtre__: Alle løvnoder har ca. samme dybde __Komplett binærtre__: Alle løvnoder har nøyaktig samme dybde #### Heaps En Max-heap er et komplett binærtre som har Max-heap-egenskapen, nemlig at alle barn har mindre verdi. En Min-heap er tilsvarende. Denne egenskapen bruker en når en tar ut det største elementet fra heapen. En vet at det øverste elementet er størst, og for så å sette det nest-øverste elementet på toppen av heapen må en gjøre $\log n$ sammenligninger. På grunn av denne egenskapen brukes en heap i prioritetskøer og heapsort. Metodene for heap inkluderer: || __Metode__ || __Kjøretid__ || || Build-max-heap || $O(n)$ || || Extract-max || $O(\log n)$ || || Max-heapify || $O(\log n)$ || || Max-heap-insert || $O(\log n)$ || || Heap-increase-key || $O(\log n)$ || || Heap-maximum || $\Theta(1)$ ||  Over er et eksempel på en Max-heap. ## Representasjon av grafer Når en skal representere en graf på en datamaskin krever en et rammeverk som støtter "pekerne" og "objektene" som en graf beskriver. De 2 vanligste måtene å gjøre dette er ved bruk av __nabolister__ eller __nabomatriser__. ### Nabolister Gitt at vi har en graf G med noder $V = \{A,B,C,D\}$ kan vi representere hvem som er nabo med hvem på følgende måte: $$A: [B, C] \\ B:[A, C] \\ C:[D]$$ Dette angir at det går en kant fra noden før kolon til hver av nodene i listen etter kolon. Denne måten å representere grafer på passer godt når grafen har få kanter (sparse). ### Nabomatriser Når vi har mange kanter i en graf (dense), velger vi gjerne å representere dette ved en nabomatrise. For en graf med $|V|$ noder, er dette en $(|V| \times |V|)$-matrise. Eksempel: 0 1 2 3 4 5 ------------- 0 | 0 1 0 0 0 1 1 | 0 0 1 1 0 1 2 | 1 1 0 1 0 0 3 | 0 0 1 0 1 0 4 | 0 0 0 0 0 1 5 | 1 0 1 0 1 0 Denne matrisa representerer en graf G med noder $V = \{0,1,2,3,4,5\}$ og kanter angitt med et entall dersom det går en kant mellom to noder. Nabomatriser kan vi også modifisere til å representere vektede grafer. Dersom det går en kant mellom $u,v$ med vekt $w(u,v) = 3$ lar vi det stå 3 på den korresponderende plassen i matrisa. # Søk i Graf / Traversering Vi ønsker en veldefinert måte å gå gjennom alle nodene i en graf, nemlig å __traversere__ en graf. De to vanligste måtene å gjøre dette på heter dybde først søk og bredde først søk. For både Bredde-Først søk (BFS) og Dybde-Først søk (DFS) kan vi terminere søket når vi finner elementet vi leter etter. ### Bredde først (BFS) Bredde først søk er en FIFO graftraverseringsalgoritme/søkealgoritme. For hver node en besøker legger en alle nodens barn i en __kø__. Mer konkret: 1. Legg til startnode i køen vår, Q. 2. Hent ny aktiv node gjennom et POP-kall til køen. 3. Legg den aktive nodens barn til i Q, så fremt de ikke allerede er besøkt. 4. Gå til steg 2 og gjenta til Q er tom. Kjøretid: $O(|V| + |E|)$ ### Dybde først (DFS) Dybde først søk er en LIFO graftraverseringsalgoritme/søkealgoritme. For hver node en besøker legger en nodens barn i en __stack__. Mer konkret: 1. Legg til startnoden i stakken, S. 2. Hent ny aktiv node gjennom POP-kall til stakken. 3. Legg den aktive nodens barn til i S, så fremt de ikke allerede er besøkt. 4. Gå til steg 2 og gjenta til S er tom. Kjøretid: $O(|V| + |E|)$ #### Topologisk sortering Ved å merke start- og slutt-tider kan DFS brukes til topologisk sortering, men dette krever da at grafen er en DAG (Directed Acyclic Graph). Finnes det en kant $(u, v)$ , skal noden $u$ komme før $v$ i ordningen. DFS brukes til å finne denne ordningen. Hvis det er mulig å lage en topologisk sortering (grafen er rettet og asyklisk), kan en kjøre [DAG-shortest-path](#dag-shortest-path), den meste effektive løsningen av korteste vei en til alle. #### In-Order, Pre-Order og Post-Order traversering In-order, Pre-order og Post-order traversering besøker hver node i et tre ved å rekursivt besøke hver nodes barn (både høyre og venstre). En grei måte å huske det på, er å tenke når vi legger nodene inn i lista over besøkte noder. Vi starter alltid i toppnoden og går nedover venstre side av grafen sånn som i visualiseringa under. I pre-order rekkefølge legger vi noden til lista når vi passerer dem på venstre side. || Pre-order ||  || F, B, A, D, C, E, G, I, H || I in-order rekkefølge legger vi noden til lista når vi er rett på undersida av noden. || In-order ||  || A, B, C, D, E, F, G, H, I || I post-order rekkefølge legger vi noden til lista når vi passerer dem på høyre side. || Post-order ||  || A, C, E, D, B, H, I, G, F || #### Kant-klassifisering __Tree-Edge__ er en kant til en direkte etterfølger. __Forward-Edge__ er en kant til en indirekte etterfølger. __Back-Edge__ er en kant til en forgjenger. __Cross-Edge__ er en kant til en node som hverken er en etterfølger eller forgjenger. # Grafalgoritmer ## Minimale spenntrær Et minimalt spenntre er et tre som er innom alle nodene nøyaktig én gang, og som har den lavest mulige kombinerte kantvekten. ### Kruskal Kruskals algoritme lager treet ved å finne de minste kantene i grafen en etter en, og lage en skog av trær. Deretter settes disse trærne gradvis sammen til ett tre, som blir det minimale spenntreet. Først finnes kanten i grafen med lavest vekt. Denne kanten legges til et tre. Deretter ser algoritmen etter den neste laveste kantvekten. Er ingen av nodene til denne kanten med i noe tre, så lages et nytt tre. Er én av nodene knyttet til et tre, så legges kanten til i det eksisterende treet. Er begge nodene knyttet til hver sitt tre settes de to trærne sammen. Er begge nodene knyttet til samme tre ignoreres kanten. Sånn fortsetter det til vi har ett tre. || __Best Case__ || __Average Case__ || __Worst Case__ || || || || $O(E \log V)$|| ### Prim Prims algoritme lager treet ved å starte i en vilkårlig node, og så legge til den kanten knyttet til noden som har lavest verdi. Deretter velges kanten med lavest verdi som er i knyttet til én av nodene som nå er en del av treet. Dette fortsetter til alle nodene er blitt en del av treet. Kjøretiden avhenger av datastrukteren som velges, pensum bruker en binærheap. || __Best Case__ || __Average Case__ || __Worst Case__ || || || || $O(E \log V)$|| ## Korteste Vei En til Alle (SSSP) Å finne korteste vei i en graf kan modellere veldig mange situasjoner i virkeligheten. Generelt deles korteste vei-problemer inn i mindre delproblemer, der en ser på korteste delstrekninger. Altså har problemet __optimal substruktur__. Visse egenskaper ved grafen vil påvirke hvilken algoritme vi bør bruke. * Er grafen rettet og uten sykler? -> Vi kan bruke DAG * Inneholder grafen kun positive kanter? -> Vi kan bruke Dijkstra * Dannes det negative sykler? "Korteste" vei er udefinert og vi må bruke Bellman-Ford. De følgende algoritmene løser problemet "korteste vei, en til alle". #### Bellman-Ford Bellman-Ford er den tregeste algoritmen, men fungerer med negative sykler. I en graf med negative sykler er korteste vei udefinert, men BF vil da vite med sikkerhet at grafen inneholder minst en negativ sykel som kan nåes fra opprinnelsesnoden (origin). BELLMAN-FORD(G, w, s) 1 INITIALIZE-SINGLE-SOURCE(G, s) 2 for i = 1 to |G.V| - 1 3 for each (u, v) in G.E 4 RELAX(u, v, w) 5 for each (u, v) in G.E 6 if v.d > u.d + w(u, v) 7 return False 8 return G Bellman-Ford gjør $i = |V| - 1$ iterasjoner, og for hver iterasjon slakker (relaxer) den hver kant i hele grafen. Etter BF har kjørt linjene 1-4 skal alle nodene ha sin endelige kostand, og en ytterlig iterasjon (linje 5-7) skal ikke gi utslag. Hvis det gjør det har vi en negativ sykel. || __Best Case__ || __Average Case__ || __Worst Case__ || || || || $O(|V| |E|)$ || #### Dijkstras algoritme Dijkstras algoritme er raskere enn Bellman-Ford, men terminerer bare hvis kantvektene er ikke-negative. Den tillater positive sykler. Dijkstras er mest effektiv når det brukes en heap som prioritetskø, og det er også denne kjøretiden vi har listet. DIJKSTRA(G, w, s) 1 INITIALIZE-SINGLE-SOURCE(G, s) 2 S = {} 3 Q = G.V 4 while (Q != {}) 5 u = EXTRACT-MIN(Q) 6 S = S + u 7 for vertex v in G.Adj[u] 8 RELAX(u, v, w) 9 return G 1. Lag en prioritetskø Q av alle nodene i grafen. (linje 3) 2. Hent ut noden fra Q som har __lavest__ kostnad. (linje 5) 3. Slakk (relax) nabonodene til den aktive og oppdater avstandene deres. (linje 8) 4. Legg den aktive noden til i besøkte noder. (linje 6) 5. Gå til steg 2 og gjenta fram til Q er tom. || __Best Case__ || __Average Case__ || __Worst Case__ || || || || $O(|E| + |V|\log |V|)$ || #### DAG shortest path Den raskeste algoritmen for å løse problemet SSSP, For å kjøre denne må man ha en DAG (Directed Acyclic Graph). Da kan vha [DFS](#dybde-først-(dfs)) lage en topologisk sortering og slakke kantene i denne rekkefølgen. 1 DAG-SHORTEST-PATHS(G, w, s) 2 for each vertex v in G.V 3 v.d = inf # Distance 4 v.p = null # Parent 5 s.d = 0 6 for each vertex u in G.v, where G.v is topologically sorted 7 for each adjacent vertex v to u 8 if v.d > u.d + w(u, v) # Relax 9 v.d = u.d + w(u, v) 10 v.p = u || __Best Case__ || __Average Case__ || __Worst Case__ || || $\Theta(|V| + |E|)$ || $\Theta(|V| + |E|)$ || $\Theta(|V| + |E|)$ || ## Korteste Vei Alle til alle (APSP) Dette problemet er en direkte forelengelse av problemet korteste vei én til alle, for en kan jo selvfølgelig kjøre Bellman-Ford eller Dijkstra for hver node. Da får en hhv. kjøretiden $|V| O(|E||V| = O(|E||V|^2)$ og $|V|O(|E| + |V|\log |V|) = O(|V||E| + |V|^2\log |V|)$. Altså vil vi i en dense graf med negative kanter og mange kanter få en kjøretid på $O(V^4)$, fordi $|E| = |V^2|$. Floyd-Warshall reduserer dette til $O(V^3)$. Merk at i en graf med negative sykler er korteste vei ikke definert og vi kan heller ikke bruke Floyd-Warshall. #### Floyd-Warshall Funker hvis det finnes negative kanter, men ingen negative sykler. Nodene må være lagret som en nabomatrise, ikke en naboliste. Psuedokode fra wikipedia: FLOYD-WARSHALL(W): 1 n = W.rows 2 D = W 3 for k = 1 to n 4 for i = 1 to n 5 for j = 1 to n 6 d_ij = min(d_ij, d_ik + d_kj) 7 return D For hver tildeling av nodene $i$, $j$ og $k$ sjekker den om det finnes en raskere vei fra $i$ til $j$ som går gjennom $k$. || __Best Case__ || __Average Case__ || __Worst Case__ || || $\Theta(|V|^3)$ || $\Theta(|V|^3)$ || $\Theta(|V|^3)$ || Algoritmen lager matriser $D^{(k)}$ der $D^{(k)}[i][j]$ gir korteste vei fra _i_ til _j_ som kun passerer noder nummerert _k_ eller lavere. #### Transitive-Closure Gjør akkurat det samme som Floyd-Warshall, men sjekker om det finnes en vei fra $i$ til $j$ eller ikke, den er altså ikke opptatt av vektene. Samme kjøretid som FW. ## Maksimal flyt Flyt kan visualiseres ved for eksempel et rørsystem for å levere vann i en by, eller som et nettverk med ulik kapasitet på de ulike kablene. Maks flyt er hvor mye som faktisk strømmer gjennom nettverket. Det kan finnes kanter med veldig liten kapasitet som hindrer flyt, så uansett om alle de andre kantene har stor kapasitet, vil maks flyt avhenge av den minste kanten dersom det ikke er noen vei rundt den. Maksimal flyt er nådd hvis og bare hvis residualnettverket ikke har flere flytforøkende stier. ### Flytnettverk Et flytnettverk er en rettet graf, der alle kantene har en ikke-negativ kapasitet. I tillegg er det et krav at dersom det finnes en kant mellom u og v, finnes det ingen kant motsatt fra v til u. Et flytnettverk har en kilde, s, og et sluk, t. Kilden kan sees på som startnode, og sluket som sluttnode. Grafen er ikke delt, så for alle v finnes en vei s ~ v ~ t. Alle kanter bortsett fra s har en kant inn. En node, bortsett fra kilden og sluket, har like mye flyt inn som den har flyt ut. Et flytnetverk kan ha mange kilder og sluk. For å eliminere problemet, lager vi en superkilde og/eller et supersluk. Superkilden har en kant til hver av kildene, og kapasiteten på de kantene setter vi som uendelig. På samme måte lager vi supersluken. En kant fra hver av slukene, og setter kapasiteten til uendelig. Da er det et nytt nettverk, med kun en kilde og en sluk, og vi kan løse problemet som vanlig. ### Residualnettverk Residualnettverket er det som er igjen av kapasitet. Altså $$ c_f(u,v) = c(u,v) - f(u,v)$$ Å følge med på residualnettverket er nyttig. Hvis en sender 1000 liter vann fra u til v, og 300 liter fra v til u, er det nok å sende 700 liter fra u til v for å ha samme resultat. ### Augmenting path En flytøkende sti (augmenting path) er en sti fra starten til en node, som øker total flyt i nettverket. En augmenting path er en enkel sti fra s til t i residualnettverket. Per definisjon av residualnettverket kan vi øke $f(u, v)$ i en augmenting path med $c_f(u, v)$ uten å gå over begrensningene. ### Minimalt kutt Et kutt i et flytnettverk er å dele grafen i to, S og T, og se på flyten gjennom kuttet. Altså $$ f(S,T) = \sum_{s \in S}\sum_{t \in T} f(u,v) - \sum_{s \in S}\sum_{t \in T} f(v,u) $$ Antall mulige kutt totalt i et nettverk med n noder: $$|C| = 2^{n-2}$$ Av alle de mulige kuttene, ønsker vi å se på det kuttet som har minst flyt, da dette er "flaskehalsen" i nettverket. ### Ford-Fulkersons metode I hver iterasjon av Ford-Fulkerson finner vi en flytforøkende sti _p_, og bruker _p_ til å modifisere _f_. Merk at Ford-Fulkersons ikke spesifiserer hvordan dette implementeres. FORD-FULKERSON-METHOD(G, s, t) 1 initialize flow to 0 2 while there exists an augmenting path p in the residual network G_f 3 augment flow f along p 4 return f || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(VE^2)$ || || $O(E_f)$|| #### Edmonds-Karp Edmonds-Karp er Ford-Fulkersons metode der BFS brukes for å finne augmenting path. Dette gir en kjøretid på $O(VE^2)$. ###Heltallsteoremet Om alle kapasiteter i flytnettverket er heltall, vil Ford-Fulkersons metode finne en maks flyt med en heltallsverdi, og flyten mellom alle nabonoder vil ha en heltallsverdi. # Problemkompleksitet ## P, NP, NPC Spørsmålet knyttet til om $P=NP$ eller ikke er ett av de syv gjenværende Millennium-problemene.  Man vet at $P$ er et subsett av $NP$, men man vet ikke om $P=NP$. || P || Polynomial time || || || NP || Nondeterministic polynomial time || || || NPC || Nondeterministic polynomial time complete || || || NPH || Nondeterministic polynomial time hard || || At et problem er P, vil si at det er løsbart i polynomisk tid. Et NP-problem er et problem hvor vi gitt en løsning kan vi bevise at denne er sann (verifisere), i polynomisk tid. Dersom man klarer å falsifisere løsningen i polynomisk tid, er problemet en del av co-NP-klassen. NP-harde problemer kan ikke løses i polynomisk tid. Det sies å være en klasse av problemer som er minst like vanskelige som det vanskeligste problemet i NP-klassen. Sagt på en annen måte: problemer som lar seg redusere fra NP-problemer i polynomisk tid, men som ikke nødvendigvis lar seg verifisere i polynomisk tid med en gitt løsning. NP-harde problemer som lar seg verifisere i polynomisk tid kalles NP-komplette. ### Redusibilitets-relasjon For å forstå bevisteknikken som brukes for å bevise at et problem er NPC, er det et par begreper som må på plass. Ett av de er redusibilitets-relasjonen $\leq_P$. I denne sammenhengen brukes det for å si at et språk ($L_1$) er polynomisk-tid redusertbart til et annet språk ($L_2$): $L_1 \leq_p L_2$. Boken (Cormen m.fl) trekker frem et eksempel der førstegradsligningen $ax + b = 0$ kan transformeres til $0x^2 + ax + b = 0$. Alle gyldige løsninger for annengradsligningen er også gyldige løsninger for førstegradsligningen. Ideen bak eksempelet er å vise at et problem, X, kan reduseres til et problem, Y, slik at inputverdier for X kan løses med Y. Kan du redusere X til Y, betyr det at å løse Y krever minst like mye som å løse X, dermed må Y være minst like vanskelig å løse som X. Det er verdt å merke seg at reduskjonen ikke er gjensidig, du kan dermed ikke bruke X til å løse Y. ### Noen kjente NPC problemer Noen vanlige eksempler på problemer som er $NPC$: - Circuit-SAT - SAT - 3-CNF-SAT - Klikk-problemet (Clique) - Vertex-Cover - Hamiltonsykel (Hamilton cycle) - Travelling Salemsan (TSP) - Subset-Sum _Men hvordan kan vi bevise at et problem er NPC?_ Boken (Cormen m.fl) deler det opp i to: 1. Bevis at problemet hører til i NP-klassen. Bruk et sertifikat til å bevise at løsningen stemmer i polinomisk tid. 2. Bevis at problemet er NP-hardt. Gjøres ved polynomisk tid reduksjon. Gitt at $P \neq NP$ så kan vi si at et problem er NPC dersom det er både et NP-problem og et NP-hard-problem. Sammenhengen er illustrert i figuren under:  Gitt at du skal bevise at TSP er et NPC-problem: 1. Bevis at $TSP \in NP$. Serifikatet du bruker kan være en sekvens av n noder du skal besøke på turen. Dersom sekvensen kun består av unike noder (vi besøker ikke samme by flere ganger for eksempel), så kan vi summere opp kostnadene og verifisere om den totale kostnaden er mindre enn et gitt heltall k. 2. Bevis at TSP er NP-hard. Hvis du har satt deg litt inn i hva de ulike problemene nevnt ovenfor beskriver, så kan det hende at du kjenner igjen deler av TSP som et Ham. cycle-problem (gitt en urettet graf G, finnes det en sykel som inneholder alle nodene kun én gang, og der sluttnode = startnode). Vi vet at TSP er minst like vanskelig å løse som Ham.-sykel problemet (da Ham.-sykel er et delproblem av TSP). Gitt at vi allerede har bevist at Ham.-sykel-problemet er NP-hard, kan vi ved polynomisk-tid reduksjon bevise at også TSP er NP-hard (Kan vi redusere Ham.-sykel til TSP i polynomisk tid, er TSP NP-H). $HAM-CYCLE \leq_P TSP$. Da de aller fleste til nå _tror_ at $P \neq NP$, så følger det at NP-harde problemer ikke kan løses i polynoisk tid, ei heller NP-problemer. Klarer du derimot å bevise at $P \neq NP$ eller at $P \neq NP$, så har du krav på en rimelig stor pengepremie. # Kjøretider til pensum-algoritmer ## Sortering og velging - $n$ er antallet elementer som skal jobbes med. - $k$ er den høyeste verdien tallene kan ha. - $d$ er maks antall siffer et tall kan ha. || __Algoritme__ || __Best case__ || __Average case__ || __Worst case__ || || Insertion sort || $O(n)$ || $O(n^2)$ || $O(n^2)$ || || Selection sort || $O(n^2)$ || $O(n^2)$ || $O(n^2)$ || || Merge sort || $O(n \lg n)$ || $O(n \lg n)$ || $O(n \lg n)$ || || Heapsort || $O(n \lg n)$ || $O(n \lg n)$ || $O(n \lg n)$ || || Quicksort || $O(n \lg n)$ || $O(n \lg n)$ || $O(n^2)$ || || Bubble sort || $O(n)$ || $O(n^2)$ || $O(n^2)$ || || Bucket sort || $O(n + k)$ || $O(n + k)$ || $O(n^2)$ || || Counting sort || $O(n + k)$ || $O(n + k)$ || $O(n + k)$ || || Radix sort || $O(d(n + k))$ || $O(d(n + k))$ || $O(d(n + k))$ || || Select || $O(n)$ || $O(n)$ || $O(n)$ || || Randomized select || $O(n)$ || $O(n)$ || $O(n^2)$ || ## Heap-operasjoner || __Operasjon__ || __Tid__ || || Insert || $O(\lg n)$ || || Delete || $O(\lg n)$ || || Build || $O(n)$ || ## Graf-operasjoner || __Algoritme__ || __Best case__ || __Average case__ || __Worst case__ || || Topologisk sort || $\Theta(V + E)$ || $\Theta(V + E)$ || $\Theta(V + E)$ || || Dybde-først-søk || $O(E+V)$ || $O(E+V)$ || $O(E+V)$ || || Bredde-først-søk || $O(E+V)$ || $O(E+V)$ || $O(E+V)$ || || Prims || $O(E \lg V)$ || $O(E \lg V)$ || $O(E \lg V)$ || || Kruskals || $O(E \lg V)$ || $O(E \lg V)$ || $O(E \lg V)$ || || Bellmann-Ford || $O(VE)$ || $O(VE)$ || $O(VE)$ || || Dijkstra || $O(V \lg V + E) $ || $O(V^2)$ || $O(V^2)$ || || Floyd-Warshall || $O(V^3)$ || $O(V^3)$ || $O(V^3)$ || || DAG-shortest-path || $O(V+E)$ || $O(V+E)$ || $O(V+E)$ || # Eksempelkode i Python ## Merge sort def merge_sort(li): if len(li) < 2: # Dersom vi har en liste med ett element, returner listen, da den er sortert return li sorted_l = merge_sort(li[:len(li)//2]) sorted_r = merge_sort(li[len(li)//2:]) return merge(sorted_l, sorted_r) def merge(left, right): res = [] while len(left) > 0 or len(right) > 0: if len(left) > 0 and len(right) > 0: if left[0] <= right[0]: res.append(left.pop(0)) else: res.append(right.pop(0)) elif len(left) > 0: res.append(left.pop(0)) elif len(right) > 0: res.append(right.pop(0)) return res ## Quicksort def quicksort(li): if len(li) < 2: return li pivot = li[0] lo = [x for x in li if x < pivot] hi = [x for x in li if x > pivot] return quicksort(lo) + pivot + quicksort(hi)

def binary_search(li, value, start=0): # Dersom lista er tom, kan vi ikke finne elementet if not li: return -1 middle = len(li) // 2 middle_value = li[middle] if value == middle_value: return start + middle elif value < middle_value: # Første halvdel return binary_search(li[:middle], value, start) elif value > middle_value: # Siste halvdel return binary_search(li[middle + 1:], value, start + middle + 1) ## Dijkstra def dijkstra(G,start): #G er grafen, start er startnoden pq = PriorityQueue() # initialiserer en heap start.setDistance(0) # Initialiserer startnodens avstand pq.buildHeap([(node.getDistance(),node) for node in G]) # Lager en heap med alle nodene while not pq.isEmpty(): currentVert = pq.delMin() # velger greedy den med kortest avstand for nextVert in currentVert.getConnections(): newDist = currentVert.getDistance() + currentVert.getWeight(nextVert) #kalkulerer nye avstander if newDist < nextVert.getDistance(): nextVert.setDistance( newDist ) # oppdaterer avstandene nextVert.setPred(currentVert) # Oppdaterer foreldrene til den med kortest avstand pq.decreaseKey(nextVert,newDist) # lager heapen på nytt så de laveste kommer først. ## Bellman-Ford def bellman_ford(G, s) # G er grafen, med noder og kantvekter. s er startnoden. distance = {} parent = {} for node in G: # Initialiserer startverdier distance[node] = float('Inf') parent[node] = None distance[s]=0 # initialiserer startnoden # relax for (len(G)-1): for u in G: # fra node u for v in G[u]: # til naboene if distance[v] > distance[u] + G[u][v]: # Sjekker om avstanden er mindre distance[v] = distance[u] + G[u][v] # hvis ja, oppdaterer avstanden parent[v]=u # og oppdaterer parent # sjekk negative sykler for u in G: for v in G[u]: if distance[v] > distance[u] + G[u][v]: return False ## Floyd-Warshall def FloydWarshall(W): n = len(W) D = W PI = [[0 for i in range(n)] for j in range(n)] for i in range(n): for j in range(n): if(i==j or W[i][j] == float('inf')): PI[i][j] = None else: PI[i][j] = i for k in range(n): for i in range(n): for j in range(n): if D[i][j] > D[i][k] + D[k][j]: D[i][j] = D[i][k] + D[k][j] PI[i][j] = PI[k][j] return (D,PI)