Are you looking for an overview of all runtimes, you will find them all at the bottom, [Runtimes for Curriculum Algorithms](#runtimes-for-curriculum-algorithms). # What are algorithms? __An informal definition__: An algorithm is any _clearly defined method for calculations_ that can take a value (or a set of values) as _input_ and return a value (or a set of values) as _output_. One can also view it as a tool that can solve a defined calculation problem. When defining the problem, one has to describe which relationship is desired between input and output, for example: «_Input_: A city road map and two points. _Output_: The shortest path (measured in meters) between the tho points.» __Description of solution__: There is no general standard for describing an algorithm. You can describe it with natural language, pseudo code, as code or through hardware drawings. The only requirement is that the description is precise. __Instances__: Each collection of input-values to a problem is called an __instance__. For example can an instance of the problem above have input values such as a road map of Trondheim, and the two points are the geographic coordinates of NTNU Gløshaugen og NTNU Dragvoll. __True or False?__: An algorithm can either be __true__ or __false__. If an algorthim is _true_, it will for all possible instances defined give the correct output; for example it is only to be expected that a sorting problem will not have problems sorting all possible collections of positibe whole numbers. If it is _false_, this will not be the case. F.ex: you may have invented an algorithm that solves all sorting problems by returning the list in reverse. This will only in some instances return the correct output, but only for a subset of potential instances. # Basic Datastructures This course covers several different datastructures with respect to various problems. It is therefore important to have a general overview of the most important ones. ## Linked lists  _[Singly linked list (Public Domain, Lindisi)](https://en.wikipedia.org/wiki/Singly_linked_list#mediaviewer/File:Singly-linked-list.svg)_ A linked list is a basic linear structure that represents elements in sequence. The concept behind the structure is that the sequence of elements is conserved by each element pointing to the next in the sequence (se the figure above). Explained in code: class Node: def __init__(self): self.value = None self.next = None n1 = Node() n2 = Node() n3 = Node() n1.value = 1 n2.value = 2 n3.value = 3 n1.next = n2 n2.next = n3 With the code above the structure will be n1 -> n2 -> n3 We can also have double linked lists, where each node contains a value and a pointer both to the previous and next nodes. 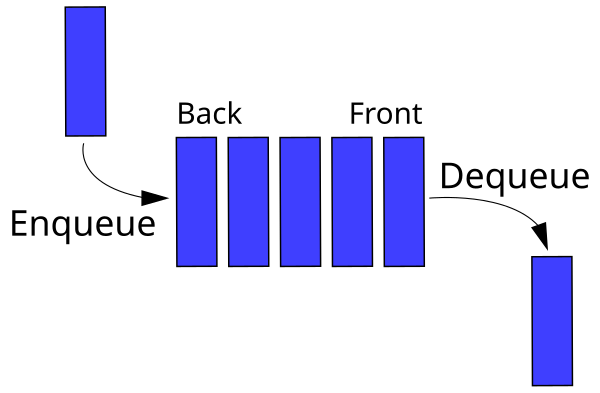### Runtimes || **Action** || **Runtime** || || Insert at the start || O(1) || || Insert at the end || O(n) || || LookUp || O(n) || || Delete element || lookUp + O(1) || ## Abstract Datastructures ### Queue A queue is an abstract datastructure that preserves the elements sequence and has two operations, _enqueue_ and _dequeue_. _Enqueue_ is the insert function, which inserts elements at the back of the queue. _Dequeue_ is the exctraction function, and retrieves the first element at the front of the queue. A queue is therefore a FIFO-datastructure (First In First Out).  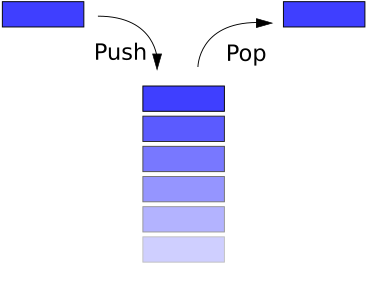### Stack A stack is an abstract datastructure which, similar to a queue, preserves the elements sequence. Unlike a queue however, a stack is LIFO (last in first out) implying that it both inserts and extracts elements from the back of the structure. These operations are called _push_ and _pop_ respectively.  ### Heap A heap is a list which can be viewed as a binary tree. A heap is an implementation of the priority tree datastructure. Check out [heapsort](#heapsort) __Max heap property:__ No node can have a higher value than its parent node. ### Hash - similar to bucket sorting. - collisions can occur as more than one object is put into a bucket Let n be the number of keys, and m be the length of the hash array. With uniform hashing the keys are distributed evenly across the m cells. The load +alpha = n/m Method: 1) Solve with linked list, at the risk of getting very long lists. 2) Solve with "open addressing", and when the bucket is full it overflows to next bucket. #### Hash functions: Division method h(k) = k mod m where m a prime number far from the power of 2. Multiplication method: h(k) = floor(m((kA)mod 1)) where 0<A<1 Key terms: linear probing, quadratic probing and perfect hashing (for the hard core) #### Runtimes( assuming single, uniform hashing and chaining): ||__Function__|| __Best Case__ || __Average Case__ || __Worst Case__ || || Failed Search || || $\Theta(1 + n/m)$ || || || x || || || || || y || || || || # Runtime Calculations Runtime is a measurement of how effective an algorithm is and is by far th emost important measurement in this course. ## About Runtimes __Why Do We Need Runtimes?:__ In a world where computers are inifitively fast and you had infinite storage space, any _true_ algorithm could be used to solve a problem - no matter how badly desgned it was. However, reality is different and therefore runtime is important. __Runtimes Explained__: A runtime describes the relationship between the size of the problem measured in input size and how long time it takes to solve it. It is possible to consider the following: The runtime will tell you that if you have a problem of a certain size, it will take so much more time if you i) insert one more element to the input or ii) double the size etc. Naturally this growth is desired to be as low as possible.

|| __Complexity__ || __Name__ || __Type__ || || $\Theta(n!)$ || Factorial || General || || $\Omega(k^n)$ || Exponential || General || || $O(n^k)$ || Polynomial || General || || $\Theta(n^3)$ || Cubic || Polynomial || || $\Theta(n^2)$ || Quadratic || Polynomial || || $\Theta(n \lg n)$ || Loglinear || Combination of linear and Polynomial || || $\Theta(n)$ || Linear || General || || $\Theta(\lg n)$ || Logarithmic || General || || $\Theta(1)$ || Constant || General || # Recursion Recursion is a problemsolving method which is based on the fact that a solution to a problem consists of the solutions to smaller instances of the same problem. This technique will be a recurring theme in several of the algorithms in the curriculum. One of the most common examples of recurisivity is the Fibonacci sequence, defined as: $$F(n) = F(n-1) + F(n-2)\\ F(0) = 0, F(1) = 1$$ Fibonacci numbers $n$ are defined as the sum of the two previous Fibonacci numbers. Good examples of recursive algorithms are _Merge_, _Quick Sort_ and _Binary search_. We also find recursive solutions through dynamic programming. ## The Master Theorem The Master Theorem is a recipe solution for finding the runtime of several reccurences. . $$ T(n) = aT(^n/_b) + f(n) \\ a \ge 1, b \gt 1 $$ This type of recurrence often occurs together with divide-and-conquer algorithms such as _Merge sort_. The problem is split up into $a$ subsets of size $^n/_b$, where f(n) work is done for the splitting and merging the results of recursive calls after they are complete. In the merge sort example, f(n) work is done to split the list into two sub-lists, then merging together the two sorted lists after the recursive calls are complete. This split happens in constant time $\Theta(1)$, while merging takes linear time $\Theta(n)$. We can therefore set $f(n) = n$. Since we at any time divide the list up into parts, each part $^n/_2$ is $a=2$ og $b=2$ respectively. For Merge sort we therefore have: $$ T(n) = 2T(^n/_2) + n $$ If we didn't already know the runtime for Merge sort, we can quickly discover it by solving this recurrence. Solving the recurrence could also be achieved by using the Master Theorem as follows: 1. Identify $a, b, f(n)$ 2. Calculate $\log_b a$ 3. Consult the following table Table over three potential outcomes of the Master Theorem: || **Case** || **Requirement** || **Solution** || || 1 || $f(n)\in O(n^{\log_b a-\epsilon})$ || $T(n) \in \Theta(n^{\log_b a})$ || || 2 || $f(n)\in \Theta(n^{\log_b a} \log^k n)$ || $T(n) \in \Theta(n^{\log_b a}\log^{k+1} n)$ || || 3 || $f(n)\in \Omega(n^{\log_b a+\epsilon})$ || $T(n) \in \Theta(f(n))$ || $\epsilon > 0$ Returning to the merge sort example. We have found $a=2, b=2, f(n)=n$, therefore $\log_b a = \log_2 2 = 1$. We are therefore in case 2, $f(n) \in \Theta(n^1)$, with the solution $T(n) \in \Theta(n\lg n)$. ### Example Another example retrieved from the 2009 Continuation Exam: Solve the following recurrence. Give the answer in asymptotic notation. Give a short explanation. $$ T(n) = 2T(^n/_3) + ^1/_n $$ We have $a = 2, b = 3, f(n) = n^{-1}$. This gives us $\log_b a = \log_3 2 \approx 0.63$. Since $f(n) = n^{-1}$ is $O(n^{.63})$, leaving us in case 1 and the solution $T(n) \in \Theta(n^{.63})$. # Sorting and Search Sorting and search are two problems that either occur as stand alone problems or as a subproblem. Sorting implies organizing a set of elements into a specific order. Searching implies that we are looking to find a certain element in a set of elements. ## Search Finding a specific element in a datastructure is a common problem. In a list of numbers we can search for the median, or a certain number. In a graf we may want to search for a way to get from one element to another. Searching algorithms for graphs (DFS and BFS) can be found under [Graph-algorithms](#graphs-and-graphalgorithms). To search in lists we have two primary methods: _Brute Force_ and _Binary Search_. ### Brute Force This method is pretty self explanatory. Iterate through the list (sorted or unsorted) from beginning to end and compare each element with the element you are trying to find. With $n$ elements in the list the runtime will be $O(n)$ ### Binary Search If we know that the list we are searching is sorted, we can use a different strategy. Given we are searching for value $a$ in a sorted list $L$ we start by finding the middle element and check if it is equal to the element we are searching for. If so, then we return the index and the search is complete. Otherwise, this elements value is compared to the element we are searching for. If the middle value is larger than the search term, the search continues in the subset with smaller values (left) and repeats the search process of dividing in half and checking against the middle term. Otherwise, the set of larger elements is selected and the search continues here. In Python: def binary_search(li, value, start=0): # Dersom lista er tom, kan vi ikke finne elementet if not li: return -1 middle = len(li) // 2 middle_value = li[middle] if value == middle_value: return start + middle elif value < middle_value: # Første halvdel return binary_search(li[:middle], value, start) elif value > middle_value: # Siste halvdel return binary_search(li[middle + 1:], value, start + middle + 1) Since we can ignore substantial parts of the list for each choice, the resulting run time is: || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(1)$ || $O(\log n)$ || $O(\log n)$ || ## Sorting Sorting algorithms can be categorized into two groups: Comparison based and distributed/non-comparison-based. ### Stability A sorting algorithm can be considered stable if the order of identical elements in the list that is to be sorted is preserved throughout the algorithm. Given the following list: $$[B_1, C_1, C_2, A_1]$$ Sorting it with a stable algorithm the identical elements will stay in the same order before and after the sort. $$[A_1, B_1, C_1, C_2]$$ ### Comparison Based Sorting Algorithms All sorting algorithms that are based on comparing two elements to determine which of the two are to come first in a sequence, are considered comparison based. It is proven that $\Omega(n\lg n)$ is the lower threshold for number of comparisons a comparison based algorithm hase do perform. In other words, it is impossible to produce a comparison based sorting algorithm which has a better worst-case runtime of $O(n\lg n)$. #### Merge sort Merge sort is a comparison based sorting algorithm It is also an example of a divide and conquer algorthim. || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(n\log n)$ || $O(n\log n)$ || $O(n\log n)$ || The core aspects of the algorthim is as follows: 1. Divide the unsorted list into $n$ sublists which each contain one element (a list with only one element is sorted) 2. Pairwise, merge together each sorted sublist. For all practical purposes this is implemented recursively. The function takes one parameter, the list that is to be sorted. If the list contains only one element, we return this list since it is already "sorted". If it is longer, we divide it up into two equal sublists (odd numbered lists get one larger than the other) and a recursive merge sort-call is made on each sublist. The returnvalues from each recursive call is then merged together. In Python: def merge_sort(li): if len(li) < 2: # Dersom vi har en liste med ett element, returner listen, da den er sortert return li sorted_l = merge_sort(li[:len(li)//2]) sorted_r = merge_sort(li[len(li)//2:]) return merge(sorted_l, sorted_r) def merge(left, right): res = [] while len(left) > 0 or len(right) > 0: if len(left) > 0 and len(right) > 0: if left[0] <= right[0]: res.append(left.pop(0)) else: res.append(right.pop(0)) elif len(left) > 0: res.append(left.pop(0)) elif len(right) > 0: res.append(right.pop(0)) return res The merge function runs in linear time. To analyze the runtime to Merge sort we can set up the following recurrence: $$T(n) = 2T(n/2) + n$$ In other words it will take twice as long to sort a list of length $^n/_2$ plus the time it takes to merge the two lists. See [Mastertheorem](#mastertheorem) for how we can solve this recursive problem and find the runtime $O(n\log n)$. Most implementations of Merge Sort are stable. As a result of the algorithm continuously producing new sublists, it requires $O(n)$ extra memory space. #### Quicksort Quicksort is a comparison based sorting algorithm that also uses divide and conquer tactics. || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(n\log n)$ || $O(n\log n)$ || $O(n^2)$ || Similar to [Merge Sort](#merge-sort), Quicksort divides the problem into smaller parts and then recursivesly solves. The quicksort function takes one parameter, the list that is to be sorted. The concept is as follows: 1. Only one element in the list? In this case the list is sorted and is to be returned. 2. Select a pivot element, the easiest being the first element in the list. 3. Create two lists, one (lo) which contains the elements from the original list that are smaller than the pivot element, and (hi) that contains all elements larger than the pivot. 4. Recursively sort lo and hi with Quicksort, returning: lo + pivot + hi In Python: def quicksort(li): if len(li) < 2: return li pivot = li[0] lo = [x for x in li if x < pivot] hi = [x for x in li if x > pivot] return quicksort(lo) + pivot + quicksort(hi) Calculating runtime for Quicksort will be somewhat more difficult than for Merge Sort as the size of the lists that are returned recursively depend on the selected pivot. Selecting a good pivot is an art in itself. The naïve method of consistently selecting the first element, kan easily be exploited by an adversary, by giving a list that is a reversed sorted list. In this case the runtime will be $n^2$. We can counter this by selecting an arbitrary pivot each time instead. #### Bubblesort Traverses the list, comparing two and two elements and swapping places if necessary. Note the algorithim has to run through the list several times, worst case n times. || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(n)$ || $O(n^2)$ || $O(n^2)$ || #### Insertion Sort Most common way for humans to sort cards. Take the first element, and place in an empty "sorted" list. Select the next unsorted element and place it accordingly to the first element depending on value. Iteratively insert element _i_ from unsorted list into the correct place in the already sorted list of _i_-1 elements. || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(n)$ || $O(n^2)$ || $O(n^2)$ || #### Selection sort A terrible sorting algoritmm which searches through the entire list and selects the smallest element each time. || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(n^2)$ || $O(n^2)$ || $O(n^2)$ || ### Other Sorting Algorithms Sorting algorithms that are not comparison based are not limited to having $O(n\lg n)$ as lower runtime threshhold. The prerequisite for these algrothims is that certain set attributes are already known before sorting. #### Heapsort There are several methods of orgainzing a heap. A max-heap is a binary tree where each node value is never higher than its parents value. A min-heap is hte opposite, where no node is allowed a lower value than its parent. A heap can be built in $O(n)$ time. Methods for heap include: || __Method__ || __Runtime__ || || Build-max-heap || $O(n)$ || || Extract-max || $O(\log n)$ || || Max-heapify || $O(\log n)$ || || Max-heap-insert || $O(\log n)$ || || Heap-increase-key || $O(\log n)$ || || Heap-maximum || $\Theta(1)$ || Heapsort builds a heap og places the highest element at the end of the list and maintains the heap with max-heapify. || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(n \log n)$ || $O(n \log n)$ || $O(n \log n)$ || #### Counting sort This algorithm assumes that an input is a whole number from a defined interval _k_. Counting sort counts how many elements which are less than or equal to the element which is to be sorted, and puts it into the correct place in th elist. This is a stable search algorithm. || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(n + k)$ || $O(n + k)$ || $O(n + k)$ || If $ k = O(n)$ , the runtime will be $ \Theta(n)$ #### Radix sort Radix sort assumes that the input is _n_ elements with _d_ digits, where each digit can have up to _k_ different values. The algorithm starts usually with the least significant digit and sorts the list according to this value before moving on to the second least significant digit. If the sorting is based on a stable algorithm that sorts in $\Theta(n+k)$ (f.ex counting sort), the entire algorthim will use $\Theta(d(n+k))$ time. || __Best Case__ || __Average Case__ || __Worst Case__ || || || || $\Theta(d(n+k))$ || #### Bucket sort Bucket sort assumes that the input is generated from an arbitrary process that distributes the elements unifromly and independently across an intervall. Bucket sort divides the interval into _n_ equally large buckets and distributes the _n_ input values into the buckets. Each bucket is then individually sorted by using a sorting algorithm such as another bucket sort, insertion sort etc. || __Best Case__ || __Average Case__ || __Worst Case__ || || || $\Theta(n)$ || $\Theta(n^2)$ || #### Topological Sort Topological sort is a sorting algorithm that is used to organize the nodes into a Directed Acyclic Graph (DAG). If there exists an edge $(u, v)$, then the node $u$ must come before $v$ in the sequence. DFS is used to find this sequence. # Graphs and Graph Algorithms A graph is a mathematical structure that is used to model _pairwise relations between objects_. In other words: a graph is an overview over several small relations. In this course graphs are some of the most important datastructures and has several accompanying algorithms. 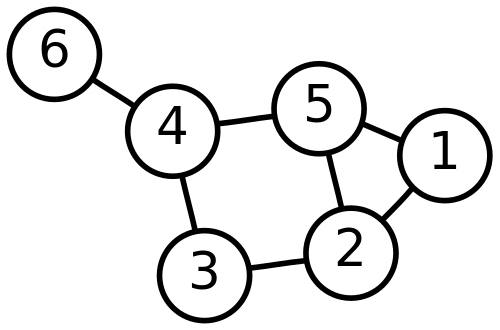## Representation A graph can look like this:  How can wi represent this on a computer? In larger systems it can be relevant to do this object oriented, where an object representing a graph containts node objects which have pointers to neighbouring node objects. A more common method is through neighborlists or matrices. ### Neighbor Lists Given the graf G with nodes $V = \{A,B,C,D\}$ we can represent which nodes are neighbors in the following manner: $$A: [B, C] \\ B:[A, C] \\ C:[D]$$ This implies that there is an edge from the node before the colon (":") to each of te nodes in the list after the colon. This method of representing graphs fits well when a graph is _sparse_, meaning has few edges. ### Neighbor Matrices When we have several edgesin a graph (dense graphs), it is preferrable to represent this via a neighbor matrix. For a graph with $|V|$ nodes, this would need a $(|V| \times |V|)$-matrix. Example: 0 1 2 3 4 5 ------------- 0 | 0 1 0 0 0 1 1 | 0 0 1 1 0 1 2 | 1 1 0 1 0 0 3 | 0 0 1 0 1 0 4 | 0 0 0 0 0 1 5 | 1 0 1 0 1 0 This matrix represents a graph G with nodes $V = \{0,1,2,3,4,5\}$ and edges given with a "1" if an edge exists between two nodes. Neighbor matrices can also be modified to represent weighted graphs where the an edge $u,v$ with weight $w(u,v) = 3$ is represented with a 3 in the corresponding cell. ## Traversal With a representation of a graph on the computer, it is now possible to traverse the elements of the matrix from beginning to end much like we traverse a list. The two most common methods of traversal are Breadth First Search (BFS) and Depth First Search (DFS). ### Breadth First Search (BFS) Breadth first search is a graph treversal algorithm that as it examines a node, it adds all of that nodes children to the queue. More precisely: 1. Given a graph, a start node and an order to insert nodes, we create a queue and place the start node into that queue. The queue has at the moment only one element. 2. As long as there is one or more elements in the queue, remove the first element from the queue (dequeue), potentially do something with the node, and add its neighbors to the queue in the order specified. If you are searching for an element, the search can be terminated when the node you are searching for is found and dequeued. Runtime: $O(|V| + |E|)$ #### Note on Traversal When traversing breadth first write out nodes for each level in the tree from left to right. ### Depth First Search (DFS) DFS uses a stack instead of a queue Since a stack is LIFO, you push the children to the topmost node onto the stack until reaching a leaf node (dead end). The topmost node is then popped, handled and discarded before moving to the underlying node. More precisely: 1. Given a graf, a starting node and an order to stack nodes, we create a stack and push the start node onto it. 2. As long as there is one or more elements on the stack, pop the top element, and push the children onto the stack, in oposite orider. If the order of the children is A, B, C, then they are pushed onto the stack, C, B, A. It is worth noting that by recording start and end times, DFS can be used for [topological sorting](#topological-sort). Runtime: $O(|V| + |E|)$ #### Traversering In-order, Pre-order og Post-order traversal visits each node in a tree by recursively visiting each nodes children from left to right. One good way of remembering this is to think about when we insert the nodes into the list of visited nodes. We always start with the toppnode and then go down the left side of the graph, visualized below. In a pre-order traversal, we place the nodes into the list as we psas them on the left hand side down. In the in-order traversal, we place the nodes into the list as we go through the node. In the post-order traversal, we place the nodes into the list as we pass them on the right hand side up. || __Traversersalmethod__ || __Visualization__ || __Result__ || || Pre-order ||  || F, B, A, D, C, E, G, I, H || || In-order ||  || A, B, C, D, E, F, G, H, I || || Post-order ||  || A, C, E, D, B, H, I, G, F || ## Minimal Spanning Trees A minimal spanning tree is a tree that is within all the nodes exactly once, and has the lowest possible cumulative edge weight. ### Kruskal Kruskal's algorithm creates a tree by finding the smallest edges in the graph one by one, and creating a forest of trees. These trees are gradually merged together into one tree which becomes the minimal spanning tree. First the edge with the smallest weight is found and this edge is made into a tree. Then the algorithm looks for the second smallest edge weight and connects these two nodes. If these were two free nodes they are connected as a new tree; if one of them are connected to an existing tree, the second node is attached to that tree; and if both are in separate trees these two trees are merged; if both are in the same tree then the edge is ignored. This method continues until we have one complete tree with all nodes. || __Best Case__ || __Average Case__ || __Worst Case__ || || || || $O(E \log V)$|| ### Prim Prim's algorithm creates a tree by starting in an arbitrary node and then adding the edge (and connecting node) with the smallest weight to tree. With now two nodes connected, the edge with the lowest weight that connects to either of the two nodes is added. This continues until all of the nodes have become a part of the tree. Runtime depends on the underlying datastructure, however the curriculum uses a binary heap. || __Best Case__ || __Average Case__ || __Worst Case__ || || || || $O(E \log V)$|| ## Shortest Path Finding the shortest path is a common problem. For example if one is to drive the shortest (in meters) from one place to another, or to find the path through an electrical circuit with the smallest cumulative resistance. In general, shortest path problems are divided into subproblems where we look at the shortest stretches between nodes. Typical issues of concern when selecting an algorithm is: * Is the graph directed or undirected (ordinary)? * Do cycles exist in the directed graph? If so, there will always be a shorter path that does not include the cycle. * Are there negative edges? * Are negative cycles created? In this case, it becomes impossible to reach certain nodes. ### One-to-All It is often important to know how a graph can be traversed, and find the distance between one and several nodes. #### Relax Assumes a list of distances to for now best routes to each node (v.d) and which node one would be coming from (v.π). Relax checks if the edge from _u_ to _v_ gives an improvement, and in that case updates the estimates _v.d = u.d+w(u,v)_ and _v.π = u_. #### Dijkstra's algorithm Dijkstra's algorithm only works if all edges are non-negative. || __Best Case__ || __Average Case__ || __Worst Case__ || || || || $O(|E| + |V|\log |V|)$ || If there exist negative cycles, this algorithm will not termniate as normal. It is possible to add an alternative stopping method, however the result may be wrong. Dijkstra is most effective when used in a heap. Implementation in other structures can cost higher runtimes and are not curriculum. How it works: 1. Initialize distances. Set the startnode to 0 and all others to +inf 2. Initialize visited. Set the startnode to visited, and all other to not visited. 3. Look at all neighbors, calculate distances and update distances. 4. Update distances. 5. Go to the node with the lowest distance value from start, and mark it as read. 6. Repeat steps 3-5 until all nodes are visited or an specific end node is visited. In python: def dijkstra(G,start): #G er grafen, start er startnoden pq = PriorityQueue() # initialiserer en heap start.setDistance(0) # Initialiserer startnodens avstand pq.buildHeap([(node.getDistance(),node) for node in G]) # Lager en heap med alle nodene while not pq.isEmpty(): currentVert = pq.delMin() # velger greedy den med kortest avstand for nextVert in currentVert.getConnections(): newDist = currentVert.getDistance() + currentVert.getWeight(nextVert) #kalkulerer nye avstander if newDist < nextVert.getDistance(): nextVert.setDistance( newDist ) # oppdaterer avstandene nextVert.setPred(currentVert) # Oppdaterer foreldrene til den med kortest avstand pq.decreaseKey(nextVert,newDist) # lager heapen på nytt så de laveste kommer først. #### Bellman-Ford Unlike Dijkstra, Bellman-Ford works also with negative edges. || __Best Case__ || __Average Case__ || __Worst Case__ || || || || $O(|V| |E|)$ || Bellman-Ford is defined recursively. In contrast to Dijkstra, Bellman-Ford relaxes all edges, meaning it updates all edges for each iteration. This helps discover any potential negative cycles. All edges are relaxed $V - 1$ times and it is after this it tests if there are any negative cycles. How it works: 1. Initialize the algorithm by setting the distance from the startnode to 0, and all others to +inf. 2. Compare all distances, and update each node with the new distance. 3. Check for negative cycles. In python: def bellman_ford(G, s) # G er grafen, med noder og kantvekter. s er startnoden. distance = {} parent = {} for node in G: # Initialiserer startverdier distance[node] = float('Inf') parent[node] = None distance[s]=0 # initialiserer startnoden # relax for (len(G)-1): for u in G: # fra node u for v in G[u]: # til naboene if distance[v] > distance[u] + G[u][v]: # Sjekker om avstanden er mindre distance[v] = distance[u] + G[u][v] # hvis ja, oppdaterer avstanden parent[v]=u # og oppdaterer parent # sjekk negative sykler for u in G: for v in G[u]: if distance[v] > distance[u] + G[u][v]: return False #### DAG shortest path The shortest path from one to all. With a given DAG it is possible to do a [topological Sort](#topological-sort) before traversing the sorted graph and relaxing all edges that are traversed. Psuedocode from Cormen: 1 DAG-SHORTEST-PATHS(G, w, s) 2 for each vertex v in G.V 3 v.d = inf # Distance 4 v.p = null # Parent 5 s.d = 0 6 for each vertex u in G.v, where G.v is topologically sorted 7 for each adjacent vertex v to u 8 if v.d > u.d + w(u, v) # Relax 9 v.d = u.d + w(u, v) 10 v.p = u || __Best Case__ || __Average Case__ || __Worst Case__ || || $\Theta(|V| + |E|)$ || $\Theta(|V| + |E|)$ || $\Theta(|V| + |E|)$ || ### All to All #### Floyd-Warshall FW works even if there are negative edges, but no negative cycles. The nodes must be stored as a neigbor matrix not a list. Psuedocode from wikipedia: 1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity) 2 for each vertex v 3 dist[v][v] ← 0 4 for each edge (u,v) 5 dist[u][v] ← w(u,v) // the weight of the edge (u,v) 6 for k from 1 to |V| 7 for i from 1 to |V| 8 for j from 1 to |V| 9 if dist[i][j] > dist[i][k] + dist[k][j] 10 dist[i][j] ← dist[i][k] + dist[k][j] 11 end if In Python: def FloydWarshall(W): n = len(W) D = W PI = [[0 for i in range(n)] for j in range(n)] for i in range(n): for j in range(n): if(i==j or W[i][j] == float('inf')): PI[i][j] = None else: PI[i][j] = i for k in range(n): for i in range(n): for j in range(n): if D[i][j] > D[i][k] + D[k][j]: D[i][j] = D[i][k] + D[k][j] PI[i][j] = PI[k][j] return (D,PI) || __Best Case__ || __Average Case__ || __Worst Case__ || || $\Theta(|V|^3)$ || $\Theta(|V|^3)$ || $\Theta(|V|^3)$ || The Algorithm creates matrix $D^{(k)}$ where $D^{(k)}[i][j]$ gives the shortest path from _i_ to _j_ which just passes nodes numbered _k_ or less. ## Max Flow Flow can be visualized by forexample a pipe system to deliver water to a city, or as a network with differing capacity on the various cables. Max fow is the maxium net capacity that actually flows through the network. There may exist some critical pipes (edges) with very low capacity, bottlenecking the entire network no matter the size of the other pipes. Max flow is achieved when there exists no more augumenting paths. ### Flow Network A flow network is a directed graf where all the edges have a non-negative capacity. Additionally, it is required that if there exists an edge between u and v, there exists no edge in the opposite direction from v to u. A flow network has a source, s, and a sink, t. The source can be seen as the starting node and the sink as the end node. The graph is not divided so for all v there exists a route s ~v~t. All nodes except from s have atleast one inbound edge. All nodes except the source and the sink have a net flow of 0 (all inbound flow = all outbound flow). A flow network can have several sources and sinks. To eliminate this problem, a super source and super sink are created and linked up to all respective sources and sinks with edges that have infinite capactiy. This new network with only one source and sink is much easier to solve. ### Residual Network The residual network is the capacity left over: $$ c_f(u,v) = c(u,v) - f(u,v)$$ To keep an eye on the residual network is useful. If we send 1000 liters of water from u to v, and 300 liters from v to u, it is enough as sending 700 from u to v to achieve the same result. ### Augumenting Path An augumenting path is a path from the source to the sink that increases the total flow in the network. It can be found by looking at the residual netowrk. ### Minimal cut A cut in a flow network divides the graph in two, S and T. It is useful to look at the flow through this cut: $$ f(S,T) = \sum_{s \in S}\sum_{t \in T} f(u,v) - \sum_{s \in S}\sum_{t \in T} f(v,u) $$ The number of potential cuts in a network with n nodes is: $$|C| = 2^{n-2}$$ Of all possible cuts, we want to see the cut with the smallest flow, as this is the bottleneck of the network. Proof exists that show that finding the minimal cut simultaneously gives us the maximum flow through the network. #### Ford-Fulkersons method Given flow _f_, in each iteration of Ford-Fulkerson we find an augumenting path _p_, and use _p_ to modify _f_. || __Best Case__ || __Average Case__ || __Worst Case__ || || $O(V*E^2)$ || || $O(E_f)$|| #### Edmonds-Karp Edmonds-Karp is Ford-Fulkerson's method where BFS is the traversal method. This ensures a runtime of $O(V*E^2)$. ### Whole Number Theorem If all capacities in the flow network are whole numbers, then Ford-Fulkerson's method will find a max flow with a whole number value, and the flow between all neighbor nodes will have whole number values. # Dynamic Programming Dynamic programming divides up problems into smaller subproblems, just like divide and conquer. DP is used when: - optimal substructure: - these subproblems overlap It is often possible to use divide and conquer on these types of problems, but must often a lot of redundant work is done as the same subproblem has to be solved several times. DP solves the subproblem once, and then uses the result each time it is needed. DP is usually used for __Optimization problems__, but as there are several optimal solutions its _an_ optimal solution. 4 Steps: 1. Characterize the strucutre of the optimal solution. 2. Recursively define the value of an optimal solution. 3. Compute the value of an optimal solution, typically in a bottom up fashion. 4. Construct an optimal solution from computed information. ## Longest common substring Is solved by DP from the bottom up, by looking at the last element i each list. ## Rod-cutting Given a rod with length n, and a list of prices for all lengtsh shorter than n. Decide the max profit you can achieve by cutting the rod up and selling it. We can cut up a rod on length _n_ in $2^(n-1)$ different ways, since we have an independendt option of cutting or not cutting at distance i inches from the left end for i = 1,2,...,n-1. # Greedy Algorithms Some times a DP is a bit overkill. Greedy algorithms choose the solution that seems the best righ tthen and there, and moves on. This does not always leed to the best solution, but for many problems this works fine. Minimal spanning trees is an example of a greedy method. Greedy algorithms solve the problem if it has the following attributes: - $Greedy-choice\ property$ We can make a choice that seems optimal at the time and solve the subproblems that occur later. The greedy choices can not be dependent on future choices nor all existing solutions. It simply iteratively takes greedy choices and reduces the given problem to a smaller one. - $Optimal\ substructure$ Optimal solitions to a problem incorporate optimal solutions to related subproblems, which we may solve independently. ## Planning activities Choose as many non-overlapping activities as possible. Assume that they are sorted by ending time and use a greedy algorithm to select them. ## Huffman's algorithm Huffman's algorithm is a greedy algorithm with the intent to minimize saving space to a known sequence of symbols. Each symbol can be represented by a binary code. The given code is dependent on the frequency the symbol, where the more frequent terms get the shorter bits. Depending on term distribution, this reduces the space required by 20-90%. Huffman is performed by always summing the two nodes with the smallest frequency values, and then using the num of these as the value of a new node. By branching left with $0$s and branching right with $1$ all symbols will be able to be represented with unique binary codes. The symbols that are most frequent will recieve shorter codes than the sparse ones. Runtime: || __Best case__ || __Average case__ || __Worst case__ || || $O(n \lg n)$ || $O(n \lg n)$ || $O(n \lg n)$ || One version of Huffmann coding can look like this:  # Multithreading ## The basics of Multithreading ###Concurrency keywords - __Spawn__ - used to start a parallel thread, allowing tha parent thread to continue with the next line while the child thread runs its subproblem - __Sync__ - A procedure cannot safely use the values returned by its spawned children until after it executes a sync statement. This keyword indicates that the program must wait until both threads are finished allowing for the correct variables to syncronize - __Serializaion__ - the serial algorithm that results from deleting the multithreaded keywords: spawn, sync, and parallel. - __Nested parallelism__ - occurs when the keyword _spawn_ precedes a procedure call. A child thread is spawned to solve the subproblem which in turn runs their own spawn subproblems, potentially creating a vast tree of subcomputations, all excecuting in parallel. - __ Logical parallelism__ - concurrency keywords express logical parallelsism, indicating which parts of the computation may procedd in parallel. At runtime it is upt o a __scheduler__ to determine which subcomputations actually run concurrently. # Problem Complexity ## P, NP, NPC The question connected to whether $P$ = $NP$ is not one of the seven remaining Millennium-problems.  We know that $P$ is a subset of $NP$, but we do not know if $P=NP$. || P || Polynomial time || || || NP || Nondeterministic polynomial time || || || NPC || Nondeterministic polynomial time complete || || || NPH || Nondeterministic polynomial time hard || || That a problem is P, implies it is solvable in polynomial time. An NP-problem is a problem that we can prove is true (verifiable), at polynomial time. If it is possible to falsify the solution in polynomial time, the problem is a part of the co-NP-class. NP-Hard (NPH) problems cannot be solved in polynomial time. It is said that this class of problems are atleast as difficult as the most difficult problem in the NP-class. In other terms, they are problems which can be reduced from NP-problems in polynomial time, but not necessarily allows themselves to be verified in polynomial time with a given solution. NP-hard problems that allow themselves to be verified in polynomial time are called NP-complete. ### Reducibility-relation To understand the proof technique used to prove a problem is NPC, a few definitions need to be in place. One of these is the reducibility-relation $\leq_P$. In this context it is used to say that a language ($L_1$) is polynomially reducible to another language ($L_2$): $L_1 \leq_p L_2$. Cormen et al., exemplifies that the linear equation $ax + b = 0$ can be transformed to $0x^2 + ax + b = 0$. All viable solutions for the quadratic equation are also viable solutions for the linear equation. The idea behind the example is to show that a problem, X, can be reduced to problem, Y, so that the input values for X can be solved with Y. If you can reduce X to Y, it implies that to solve Y requires atleast as much as solving X, therefore must Y be as difficult to solve as X. It is worth mentioning that this relation is not mutual, and you therefore cannot use X to solve Y. ### Some known NPC problems Some common examples of NPC problems include: - Circuit-SAT - SAT - 3-CNF-SAT - Clique-problemet - Vertex-Cover - Hamilton-Cycle - Travelling Salesman (TSP) - Subset-Sum _But how can we prove a poblem is NPC?_ Cormen et al. divides this into two parts: 1. Prove that the problem belongs to the NP-class. Use a certification to prove that the solution is verified in polynomial time. 2. Prove the problem is NP-hard. This is done through polynimial time reduction. Given $P$ != $NP$, then we can say that a problem is NPC if it is both an NP-problem and an NP-hard-problem. This connection is illustrated in the figure below:  Given that you are trying to prove that TSP is an NPC-problem: 1. Prove that TSP$\in$ NP. The certification you use can be a sequence of n nodes that you shall visit on your trip. If the sequence just consists of unique nodes (we do not visit the same city more than oce) then we can sum up the costs and verify the total cost is less than a given number _k_. 2. Prove that TSP is NP-hard. If you have understood what the different problems described above, then you will recognize that TSP is a [Hamilton Cycle](#Hamilton Cycle)-problem (given an undireted graph G, there exists a cucle that contains all the nodes only once, and where the starting node = the end node). We know that TSP is atleast as difficult to solve as a the Ham-cycle problem (as Ham-cycle is a subproblem of TSP). Given that we already have proved that the Ham-cycle problem is NP-hard, we can show with polynomial time reduction that TSP is also NP-hard (since we reduce Ham-cycle to TSP in polynimial time, then TSP is NP-H) $HAM-CYCLE \leq_P TSP$. As most people now _believe_ that $P$ != $NP$, then it follows that NP-H problems cannot be solved in polynomial time, and neither NP-problems. Disproving this, implying that $P$ != $NP$ or that $P$ = $NP$, then you have claim to a rather large sum of money. # Runtimes for curriculum algorithms ## Sorting and selection - $n$ is the number of elements that are being handled. - $k$ is the highest value possible. - $d$ is the max munber of digits an element can have. || __Algorithm__ || __Best case__ || __Average case__ || __Worst case__ || || Insertion sort || $O(n)$ || $O(n^2)$ || $O(n^2)$ || || Selection sort || $O(n^2)$ || $O(n^2)$ || $O(n^2)$ || || Merge sort || $O(n \lg n)$ || $O(n \lg n)$ || $O(n \lg n)$ || || Heapsort || $O(n \lg n)$ || $O(n \lg n)$ || $O(n \lg n)$ || || Quicksort || $O(n \lg n)$ || $O(n \lg n)$ || $O(n^2)$ || || Bubble sort || $O(n)$ || $O(n^2)$ || $O(n^2)$ || || Bucket sort || $O(n + k)$ || $O(n + k)$ || $O(n^2)$ || || Counting sort || $O(n + k)$ || $O(n + k)$ || $O(n + k)$ || || Radix sort || $O(d(n + k))$ || $O(d(n + k))$ || $O(d(n + k))$ || || Select || $O(n)$ || $O(n)$ || $O(n)$ || || Randomized select || $O(n)$ || $O(n)$ || $O(n^2)$ || ## Heap-operations || __Operations__ || __Runtime__ || || Insert || $O(\lg n)$ || || Delete || $O(\lg n)$ || || Build || $O(n)$ || ## Graph-operations || __Algorithm__ || __Best case__ || __Average case__ || __Worst case__ || || Topological sort || $\Theta(V + E)$ || $\Theta(V + E)$ || $\Theta(V + E)$ || || Depth-first-search || $O(E+V)$ || $O(E+V)$ || $O(E+V)$ || || Breadth-first-search || $O(E+V)$ || $O(E+V)$ || $O(E+V)$ || || Prim's || $O(E \lg V)$ || $O(E \lg V)$ || $O(E \lg V)$ || || Kruskal's || $O(E \lg V)$ || $O(E \lg V)$ || $O(E \lg V)$ || || Bellmann-Ford's || $O(VE)$ || $O(VE)$ || $O(VE)$ || || Dijkstra's || $O(V \lg V + E) $ || $O(V^2)$ || $O(V^2)$ || || Floyd-Warshall's || $O(V^3)$ || $O(V^3)$ || $O(V^3)$ || || DAG-shortest-path || $O(V+E)$ || $O(V+E)$ || $O(V+E)$ || ## Other algorithms